Đề ôn tập môn Toán Lớp 12 - Bài tập phương trình lôgarit
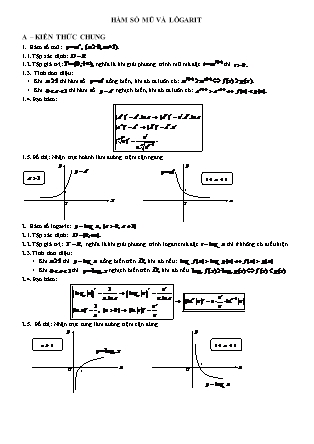
1. Hàm số mũ:
1.1.Tập xác định:
1.2.Tập giá trị: nghĩa là khi giải phương trình mũ mà đặt thì
1.3. Tính đơn điệu:
+ Khi thì hàm số đồng biến, khi đó ta luôn có:
+ Khi thì hàm số nghịch biến, khi đó ta luôn có:
1.4.Đạo hàm:
1.5.Đồ thị: Nhận trục hoành làm đường tiệm cận ngang.
2. Hàm số logarit:
2.1.Tập xác định:
2.2.Tập giá trị: , nghĩa là khi giải phương trình logarit mà đặt thì không có điều kiện.
2.3.Tính đơn điệu:
+ Khi thì đồng biến trên khi đó nếu: .
+ Khi thì nghịch biến trên khi đó nếu .
2.4.Đạo hàm:
Bạn đang xem tài liệu "Đề ôn tập môn Toán Lớp 12 - Bài tập phương trình lôgarit", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
HÀM SỐ MŨ VÀ LÔGARIT A – KIẾN THỨC CHUNG 1. Hàm số mũ: 1.1.Tập xác định: 1.2.Tập giá trị: nghĩa là khi giải phương trình mũ mà đặt thì 1.3. Tính đơn điệu: + Khi thì hàm số đồng biến, khi đó ta luôn có: + Khi thì hàm số nghịch biến, khi đó ta luôn có: 1.4.Đạo hàm: 1.5.Đồ thị: Nhận trục hoành làm đường tiệm cận ngang. O 1 O 1 2. Hàm số logarit: 2.1.Tập xác định: 2.2.Tập giá trị: , nghĩa là khi giải phương trình logarit mà đặt thì không có điều kiện. 2.3.Tính đơn điệu: + Khi thì đồng biến trên khi đó nếu: . + Khi thì nghịch biến trên khi đó nếu . 2.4.Đạo hàm: 2.5. Đồ thị: Nhận trục tung làm đường tiệm cận đứng. O 1 1 O BÀI TẬP TRẮC NGHIỆM Câu 1: Tìm tập xác định của hàm số . A. . B. . C. . D. . Câu 2: Tìm tập xác định của hàm số . A. B. . C. . D. . Câu 3: Hàm sốcó tập xác định là: A. B. C. D. Câu 4: Cho . Tìm mệnh đề đúng trong các mệnh đề sau: A. Tập xác định của hàm số là khoảng . B. Tập giá trị của hàm số là tập R. C. Tập giá trị của hàm số là tập R. D. Tập xác định của hàm số là tập R. Câu 5: Tập xác định của hàm số là: A. B. C. D. Câu 6: Tập xác định của hàm số . A. . B. . C. . D. . Câu 7: Hàm số có tập xác định là A. . B. . C. . D. . Câu 8: Tập xác định là: A. B. C. D. Câu 9: Tìm tập xác định của hàm số. A. B. C. D. Câu 10: Cho tập và các hàm số , , D là tập xác định của hàm số nào? A. và B. và C. và D. và Câu 11: Tìm tập xác định của hàm số là A. B. C. D. Câu 12: Hàm số nào trong các hàm số sau có tập xác định ? A. B. C. D. Câu 13: Tìm tập xác định của hàm số A. B. C. D. Câu 14: Tìm tập xác định của hàm số A. B. C. D. Câu 15: Tập xác định của hàm số là A. . B. . C. R. D. . Câu 16: Tìm tập xác định của hàm số . A. . B. . C. . D. . Câu 17: Tìm tất cả các giá trị thực của tham số để hàm số có tập xác định ? A. B. C. D. Câu 18: Tìm tất cả các giá trị thực của tham số m để hàm số xác định trên . A. B. C. D. Câu 19: Tìm tập xác định hàm số sau:. A. . B. . C. . D. . Câu 20: Tập xác định của hàm số: là A. . B. . C. . D. . Câu 21: Cho hàm số . Khảng định nào sau đây sai A. Hàm số có tập xác định là . B. . C. Hàm số nghịch biến trên khoảng xác định. D. Đồ thị hàm số có tiệm cận đứng là trục . Câu 22: Tìm mệnh đề đúng trong các mệnh đề sau: A. Hàm số với là một hàm số nghịch biến trên khoảng . B. Đồ thị các hàm số và với đối xứng với nhau qua trục hoành. C. Hàm số với có tập xác định là . D. Hàm số với là một hàm số đồng biến trên khoảng . Câu 23: Giá trị thực của để hàm số đồng biến trên . A. . B. . C. . D. . Câu 24: Đồ thị hàm số nào sau đây đối xứng với đồ thị hàm số qua đường thẳng . A. . B. . C. . D. . Câu 25: Hàm số nào sau đây nghịch biến trên tập xác định của nó? A. B. C. D. Câu 26: Cho hàm số . Tìm để hàm số đồng biến trên khoảng . A. . B. . C. . D. . Câu 27: Tìm tất cả các giá trị của tham số để hàm số nghịch biến trên khoảng A. B. C. D. Câu 28: Tìm tập các giá trị thực của tham số để hàm số đồng biến trên khoảng. A. . B. . C. . D. . Câu 29: Tập hợp các giá trị của tham số thực để đồ thị hàm số đồng biến trên khoảng là A. . B. . C. . D. . Câu 30: Tìm các giá trị của tham số để hàm số nghịch biến trên khoảng A. B. C. D. Câu 31: Tìm tất cả các giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng A. B. . C. . D. . Câu 32: Cho hàm số . Tính tổng A. . B. . C. . D. . Câu 32: Kí hiệu . Giá trị của bằng: A. B. C. D. Câu 33: Cho với . Biết rằng . Tính giá trị của A. . B. . C. . D. . Câu 34: Cho . Nếu thì là A. . B. . C. . D. . Câu 35: Cho hàm số . Nếu thì có giá trị bằng A. . B. . C. D. .
Tài liệu đính kèm:
 de_on_tap_mon_toan_lop_12_bai_tap_phuong_trinh_logarit.docx
de_on_tap_mon_toan_lop_12_bai_tap_phuong_trinh_logarit.docx



