Đề ôn tập môn Toán Lớp 12 - Chương 3-Bài 4: Giải toán hình học không gian bằng phương pháp tọa độ
1. Để giải một bài toán bằng phương pháp toạ độ ta thực hiện theo các bước sau :
Bước 1: Thực hiện việc chọn hệ trục toạ độ thích hợp, chú ý đến vị trí của gốc O, chuyển bài toán đã cho về bài toán hình học giải tích
Bước 2: Giải bài toán hình học giải tích nói trên.
Bước 3: Chuyển các kết luận của bài toán hình học giải tích sang các tính chất hình học tương ứng.
2. Cách chọn hệ trục tọa độ Oxyz một số hình thường gặp
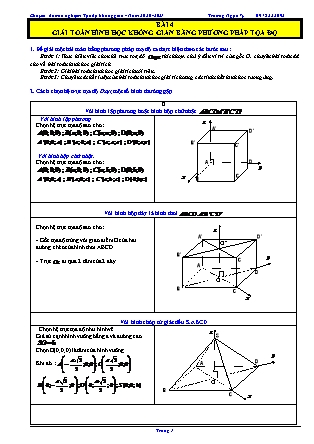
Với hình lập phương hoặc hình hộp chữ nhật
Với hình lập phương .
Chọn hệ trục tọa độ sao cho :
Với hình hộp chữ nhật.
Chọn hệ trục tọa độ sao cho :
Bạn đang xem tài liệu "Đề ôn tập môn Toán Lớp 12 - Chương 3-Bài 4: Giải toán hình học không gian bằng phương pháp tọa độ", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
BÀI 4 GIẢI TOÁN HÌNH HỌC KHÔNG GIAN BẰNG PHƯƠNG PHÁP TỌA ĐỘ 1. Để giải một bài toán bằng phương pháp toạ độ ta thực hiện theo các bước sau : Bước 1: Thực hiện việc chọn hệ trục toạ độ thích hợp, chú ý đến vị trí của gốc O, chuyển bài toán đã cho về bài toán hình học giải tích Bước 2: Giải bài toán hình học giải tích nói trên. Bước 3: Chuyển các kết luận của bài toán hình học giải tích sang các tính chất hình học tương ứng. 2. Cách chọn hệ trục tọa độ Oxyz một số hình thường gặp Với hình lập phương hoặc hình hộp chữ nhật Với hình lập phương . Chọn hệ trục tọa độ sao cho : Với hình hộp chữ nhật. Chọn hệ trục tọa độ sao cho : D’ A’ B’ C’ D A B C Với hình hộp đáy là hình thoi Chọn hệ trục tọa độ sao cho : - Gốc tọa độ trùng với giao điểm O của hai đường chéo của hình thoi ABCD - Trục đi qua 2 tâm của 2 đáy A B C D D’ C A’ B’ O O’ Với hình chóp tứ giác đều S.ABCD Chọn hệ trục tọa độ như hình vẽ Giả sử cạnh hình vuông bằng a và đường cao Chọn O(0;0;0) là tâm của hình vuông Khi đó : S O A D C B Với hình chóp tam giác đều S.ABC Chọn hệ trục tọa độ như hình vẽ Giả sử cạnh tam giác đều bằng a và đường cao bằng . Gọi I là trung điểm của BC Chọn hệ trục tọa độ như hình vẽ sao cho I(0;0;0) Khi đó : I H C B A S Với hình chóp S.ABCD có ABCD là hình chữ nhật và SA (ABCD ABCD là hình chữ nhật chiều cao bằng Chọn hệ trục tọa độ như hình vẽ sao cho A(0;0;0) Khi đó : S D A C O B Với hình chóp S.ABC có ABCD là hình thoi và SA (ABCD) ABCD là hình thoi cạnh chiều cao bằng Chọn hệ trục tọa độ như hình vẽ sao cho O(0;0;0) S C D A O B Với hình chóp S.ABC có SA (ABC) và ABC vuông tại A Tam giác ABC vuông tại A có đường cao bằng . Chọn hệ trục tọa độ như hình vẽ sao cho A(0;0;0) Khi đó : C B A S Với hình chóp S.ABC có SA (ABC) và ABC vuông tại B Tam giác ABC vuông tại B có đường cao bằng . Chọn hệ trục tọa độ như hình vẽ sao cho B(0;0;0) Khi đó : B A C S Với hình chóp S.ABC có (SAB) (ABC), SAB cân tại S và ABC vuông tại C ABC vuông tại C chiều cao bằng H là trung điểm của AB Chọn hệ trục tọa độ như hình vẽ sao cho C(0;0;0) Khi đó : ; S H C B A Với hình chóp S.ABC có (SAB) (ABC), SAB cân tại S và ABC vuông tại A ABC vuông tại A chiều cao bằng H là trung điểm của AB Chọn hệ trục tọa độ như hình vẽ sao cho A(0;0;0) Khi đó : S C B A H Với hình chóp S.ABC có (SAB) (ABC), SAB cân tại S và ABC vuông cân tại C Tam giác ABC vuông cân tại C có đường cao bằng . H là trung điểm của AB Chọn hệ trục tọa độ như hình vẽ sao cho H(0;0;0) Khi đó : A H C B S · Tính chất các trục tọa độ Trục Ox có VTCP là: Mặt phẳng có VTPT là: Và phương trình mặt phẳng : Trục Oy có VTCP là: Mặt phẳng có VTPT là: Và phương trình mặt phẳng : Trục Oz có VTCP là: Mặt phẳng có VTPT là: Và phương trình mặt phẳng : Dạng 1 HÌNH CHÓP Cho hình chóp có đáy là tam giác vuông có , vuông góc với và . Góc giữa hai ,là: A. B. C. D. Cho hình chóp tam giác đều đỉnh S, có độ dài cạnh đáy bằng a. Gọi M, N lần lượt lượt trung điểm của các cạnh SB và SC. Tính theo a diện tích của tam giác , biết rằng . A. B. C. D. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = 2a, cạnh SA vuông góc với đáy và SA = 2a. Gọi M là trung điểm SC. Tính diện tích tam giác MAB theo a. A. B. C. D. Cho hình chóp có đáy là tam giác vuông có , vuông góc với và . Tính khoảng cách giữa hai đường thẳng và với là trung điểm của cạnh . A. B. C. D. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với và SA vuông góc với mặt phẳng (ABCD) . Gọi M; N lần lượt là trung điểm của AD và SC; I là giao điểm của BM và AC. Thể tích khối tứ diện ANIB là: A. B. C. D. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N, P lần lượt là trung điểm của các cạnh SB, BC và CD. Tính thể tích khối tứ diện CMNP. A. B. C. D. Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh , cạnh bên bằng . Gọi E là điểm đối xứng của D qua trung điểm của SA, M là trung điểm của AE, N là trung điểm của BC. Tính theo khoảng cách giữa hai đường thẳng MN và AC. A. B. C. D. Cho hình tứ diện ABCD có cạnh AD vuông góc với mặt phẳng(ABC); ; ; . Khoảng cách từ điểm A đến mặt phẳng (BCD) là: A. B. C. D. Trong không gian với hệ toạ độ cho hình chóp S.ABCD có đáy ABCD là hình thoi. Đường thẳng AC cắt BD tại gốc toạ độ O. Biết ; ; . Gọi M là trung điểm của SC. Tính góc và khoảng cách giữa hai đường thẳng SA và BM A. và B. và C. và D. và Cho hai nửa đường thẳng và vuông góc với nhau và nhận là đoạn vuông góc chung. Lấy điểm M trên và điểm N trên sao cho . Xác định tâm I và tính theo bán kính R của mặt cầu ngoại tiếp tứ diện ABMN. A. và . B. và . C. và . D. và . Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ; ; và mặt phẳng (SAB) vuông góc với mặt phẳng đáy. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC . Thể tích khối chóp S.BMDN là: A. (đvtt) B. (đvtt) C. (đvtt) D. (đvtt). Cho hình chóp S.ABCD có đáy ABCD là hình thang , , , SA vuông góc với đáy và . Gọi M,N lần lượt là trung điểm của SA và SD. Tính thể tích của khối chóp S.BCNM theo . A. (đvtt) B. (đvtt) C. (đvtt) D. (đvtt). Cho hình chóp S.ABCD có đáy là hình vuông cạnh , . Mặt phẳng qua BC hợp với AC một góc 300 , cắt SA, SD lần lượt tại M, N. Tính diện tích thiết diện BCNM. A. (đvtt) B. (đvtt) C. (đvtt) D. (đvtt). Trong không gian với hệ toạ độ cho hình chóp S.ABCD có đáy ABCD là hình thoi. Đường thẳng AC cắt BD tại gốc toạ độ O. Biết ; ; . Gọi M là trung điểm của SC. Giả sử mặt phẳng (ABM) cắt đường thẳng SD tại N. Tính thể tích khối chóp S.ABMN. A. (đvtt) B. (đvtt) C. (đvtt) D. (đvtt) Cho hai nửa đường thẳng và vuông góc với nhau và nhận là đoạn vuông góc chung. Lấy điểm M trên và điểm N trên sao cho . Tính khoảng cách giữa hai đường thẳng AM và BI. A. B. C. D. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ; ; và mặt phẳng (SAB) vuông góc với mặt phẳng đáy. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC . Tính cosin của góc giữa hai đường thẳng SM, DN A. B. C. D. Cho hình chóp tứ giác đều S.ABCD có các cạnh đều bằng . Tính khoảng cách từ điểm A đến mặt phẳng (SCD). A. B. C. D. Cho hình chóp tứ giác đều S.ABCD có các cạnh đều bằng . Tính sin của góc giữa SB và mặt phẳng (SCD) A. B. C. D. Cho hình chóp S.ABCD có đáy là hình thang , , , SA vuông góc với đáy và . Gọi H là hình chiếu của A trên SB. Khoảng cách từ H đến mặt phẳng (SCD) là: A. B. C. D. Cho tứ diện OABC có đáy OBC là tam giác vuông tại O, OB=a, OC=, (a>0) và đường cao OA=. Gọi M là trung điểm của cạnh BC. Tính khoảng cách giữa hai đường thẳng AB và OM. A. B. C. D. Cho hình chóp SABC có đáy là tam giác ABC vuông cân tại A, AB = AC = a (a > 0), hình chiếu của S trên đáy trùng với trọng tâm G của DABC. Đặt SG = x (x > 0). Xác định giá trị của x để góc phẳng nhị diện (B, SA, C) bằng 60o. A. B. C. D. Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy là a. Gọi M, N là trung điểm SB, SC. Tính theo a diện tích DAMN, biết (AMN) vuông góc với (SBC). A. B. C. D. Cho hình chóp SABC có độ dài các cạnh đề bằng 1, O là trọng tâm của tam giác DABC. I là trung điểm của SO. Mặt phẳng (BIC) cắt SA tại M. Tỉ lệ là: A. B. C. D. Cho hình chóp O.ABC có đôi một vuông góc. Điểm M cố định thuộc tam giác ABC có khoảng cách lần lượt đến các mặt phẳng (OBC); (OCA); (OAB) lá 1; 2; 3. Tính để thể tích khối chóp O.ABC nhỏ nhất. A. B. C. D. Cho hình chóp A.BCD có các cạnh AB, AC, AD đôi một vuông góc. cân, cạnh bên bằng a, . Cosin góc giữa hai đường thẳng BD và DC là: A. B. C. D. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2, AC = . vuông cân tại A. K là trung điểm của cạnh SD. Hãy xác định cosin góc giữa đường thẳng CK và AB? A. B. C. D. Dạng 2 HÌNH HỘP Cho hình hộp chữ nhật ABCD.A’B’C’D’ có thể tích bằng 1. Gọi I, J, K lần lượt là trung điển của các đoạn thẳng AA’, CD v A’D’. Tính thể tích khối tứ diện BIJK. A. B. C. D. Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân với AB = AC = a, góc , cạnh bên BB' = a. Gọi I là trung điểm CC'. Tính cosin của góc giữa hai mặt phẳng (ABC) và (AB'I). A. B. C. D. Cho lăng trụ tam giác ABC.A’B’C’ có các mặt bên là hình vuông cạnh a. Gọi D, E, F lần lượt là trung điểm của các đoạn thẳng BC, A’C’, C’B’. Tính khoảng cách giữa DE và A’F. A. B. C. D. Cho hình lập phương có cạnh bằng a. Tìm khoảng cách giữa hai đường thẳng và . A. B. C. D. Trong không gian với hệ toạ độ cho hình lăng trụ đứng với ; ; ; . Viết phương trình mặt cầu có tâm là A và tiếp xúc với mặt phẳng . A. B. C. D. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông, , cạnh bên . Gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM, B’C A. B. C. D. Cho lăng trụ ABC.A'B'C' các các mặt bên đều là hình vuông cạnh a. Gọi D, F lần lượt là trung điểm của các cạnh BC, C'B'. Tính khoảng cách giữa hai đường thẳng A'B và B'C'. A. B. C. D. Cho hình lăng trụ tam giác đều có AB = a, góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 600. Tính theo a khoảng cách giữa hai mặt phẳng (ABC) và (A’B’C’) được kết quả A. B. C. D. Cho lăng trụ đứng có đáy là tam giác cân tại A, . Góc giữa (A'BC) và (ABC) là . Khoảng cách từ B' đến mp(A'BC) là: A. B. C. D. Cho lăng trụ đứng có đáy ABC là tam giác vuông cân tại B, AB = . Góc giữa cạnh và mặt đáy là 600. Tính khoảng cách từ điểm A đến mp(C) A. B. C. D. Cho lăng trụ đứng có đáy ABC là tam giác cạnh . Góc giữa mặt và mặt đáy là 300. Tính khoảng cách từ điểm A đến mp(C) A. B. C. D. Cho hình lăng trụ đứngcó đáylà tam giác vuông tại, . Gọilà trung điểm đoạn thẳngvàlà giao điểm củavà. Tính khoảng cách từ đến theo . A. B. C. D. Cho hình lăng trụ đứng có đáy là tam giác vuông cân tại có cạnh và biết . Gọi là giao điểm của và . Tính khoảng cách từ đến . A. B. C. D. Cho hình lập phương cạnh bằng a; Khoảng cách giữa và bằng A. B. C. D. Cho hình lăng trụ đứng có đáy là tam giác vuông cân tại có cạnh và biết . Tính khoảng cách giữa 2 đường thẳng và . A. B. C. D. Cho hình hộp chữ nhật có , . Tính khoảng cách giữa 2 đường thẳng và . A. B. C. D. Trong không gian với hệ tọa độ , Cho hình chóp S. ABCD có đáy ABCD là hình thoi. Gốc tọa độ là giao điểm của 2 đường chéo AC và BD. Biết . M là trung điểm của SC. Khoảng cách giữa SA và BM là: A. B. C. D. Trong không gian với hệ tọa độ , Cho hình lập phương ABCD. A’B’C’D’ biết A, . M, N lần lượt là trung điểm của AB, CD. Khoảng cách giữa MN và A’C là: A. B. C. D. Trong không gian với hệ tọa độ , Cho hình lập phương ABCD. A’B’C’D’. M, N lần lượt là trung điểm của cạnh AD và BB’. Khi đó cosin của góc giữa hai đường thẳng và là: A. B. C. 1 D. Cho hình lập phương có cạnh bằng a. Gọi M, N, P lần lượt là trung điểm các cạnh . Góc giữa hai đường thẳng MP và C’N là: A. 30o. B. 120o. C. 60o. D. 90o. Cho hình lập phương có cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm các cạnh . Góc giữa đường thẳng AC’ và mặt phẳng (MNP) là A. B. C. D.
Tài liệu đính kèm:
 de_on_tap_mon_toan_lop_12_chuong_3_bai_4_giai_toan_hinh_hoc.doc
de_on_tap_mon_toan_lop_12_chuong_3_bai_4_giai_toan_hinh_hoc.doc



