Đề kiểm tra khảo sát lần 1 môn Toán Lớp 12 - Năm học 2020-2021 - Trường THPT Lý Thái Tổ - Mã đề 320
Câu 7. Cho hàm số có và . Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng và .
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng và .
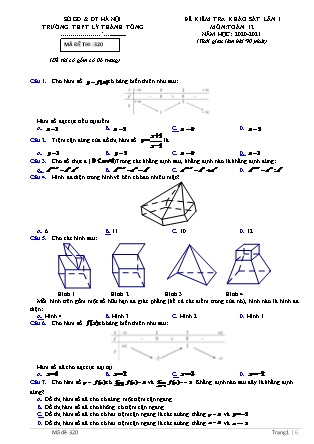
Câu 8. Cho hàm số có bảng biến thiên như sau:
Hàm số nghịch biến trên khoảng nào?
A. B. C. D.
Câu 9. Cho hàm số . Hàm số đồng biến trên khoảng nào?
A. B. C. D. và
Câu 10. Giá trị nhỏ nhất của hàm số trên đoạn [0 ; 4] bằng:
A. -4 B. 68 C. 0 D. -259
Câu 11. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
Bạn đang xem tài liệu "Đề kiểm tra khảo sát lần 1 môn Toán Lớp 12 - Năm học 2020-2021 - Trường THPT Lý Thái Tổ - Mã đề 320", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
SỞ GD & ĐT HÀ NỘI TRƯỜNG THPT LÝ THÁNH TÔNG MÃ ĐỀ THI : 320 ....................*................... ĐỀ KIỂM TRA KHẢO SÁT LẦN 1 MÔN:TOÁN 12 NĂM HỌC: 2020-2021 (Thời gian làm bài:90 phút) (Đề thi có gồm có 06 trang) Cho hàm số có bảng biến thiên như sau: Hàm số đạt cực tiểu tại điểm A. B. C. D. Tiệm cận đứng của đồ thị hàm số là A. . B. . C. . D. Cho số thực a ()Trong các khẳng định sau, khẳng định nào là khẳng định đúng: A. . B. . C. . D. . Hình đa diện trong hình vẽ bên có bao nhiêu mặt? A. 6. B. 11. C. 10. D. 12. Cho các hình sau: Hình 1 Hình 2 Hình 3 Hình 4 Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình nào là hình đa diện: A. Hình 4. B. Hình 3. C. Hình 2. D. Hình 1. Cho hàm số có bảng biến thiên như sau: Hàm số đã cho đạt cực đại tại A. B. C. D. Cho hàm số có và . Khẳng định nào sau đây là khẳng định đúng? A. Đồ thị hàm số đã cho có đúng một tiệm cận ngang. B. Đồ thị hàm số đã cho không có tiệm cận ngang. C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng và . D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng và . Cho hàm số có bảng biến thiên như sau: Hàm số nghịch biến trên khoảng nào? A. B. C. D. Cho hàm số . Hàm số đồng biến trên khoảng nào? A. B. C. D.và Giá trị nhỏ nhất của hàm số trên đoạn [0 ; 4] bằng: A. -4 B. 68 C. 0 D. -259 Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. B. C. D. Rút gọn biểu thức ta được: A. . B. . C. . D. . Mỗi đỉnh của bát diện đều là đỉnh chung của bao nhiêu mặt? A. 4. B. 5. C. 8. D. 3. Cho hàm số có bảng xét dấu đạo hàm như sau Mệnh đề nào dưới đây sai ? A. Hàm số đồng biến trên khoảng C. Hàm số đồng biến trên khoảng . B. Hàm số nghịch biến trên khoảng . D. Hàm số nghịch biến trên khoảng Khối lập phương cạnh có thể tích là: A. . B. . C. . D. . Cho hàm số liên tục trên đoan và có đồ thị như hình vẽ bên. Goi và là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn . Giá trị của bằng: A. 13 B. 12 C. 0 D. 11 Viết biểu thức () dưới dạng luỹ thừa với số mũ hữu tỷ. A. . B. . C. . D. . Cho hình lập phương có độ dài đường chéo bằng . Thể tích của khối lập phương là. A. . B. . C. . D. . Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là : A. 2. B. 0. C. 3. D. 1. Cho khối chóp có diện tích đáy và chiều cao . Thể tích của khối chóp đã cho bằng: A. . B. . C. . D. . Cho hàm số . Trong các khẳng định sau, khẳng định nào là đúng: A. Hàm số nghịch biến trên khoảng . C. Hàm số đồng biến trên khoảng . B. Hàm số nghịch biến trên khoảng . D. Hàm số đồng biến trên khoảng . Tìm giá trị thực của tham số để hàm số đạt cực tiểu tại ? A. В. C. D. Hàm số có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng? A. B. C. D. Mặt phẳng chia khối lăng trụ thành các khối đa diện nào? A.Một khối chóp tứ giác và một khối chóp tam giác. B. Một khối chóp ngũ giác và một khối chóp tứ giác. C. Hai khối chóp tứ giác. D. Hai khối chóp tam giác. Giá trị nhỏ nhất của hàm số trên đoạn bằng: A. 2. B. 3. C. 0 D. -1 Cho hàm số có bảng biến thiên như sau: Số nghiệm của phương trình là: A. 0 B. 2. C. 1 D. 3. Cho khối chóp có đáy là hình vuông cạnh và chiều cao bằng . Thể tích khối chóp đã cho bằng: A. . B. . C. . D. . Cho hàm số có đạo hàm . Số điểm cực trị của hàm số đã cho là: A. 3 B. 1 C. 5 D. 2 Xác định để hàm số có đồ thị như hình vẽ bên. Chọn đáp án đúng? A. B. C. D. Có bao nhiêu giá trị nguyên của tham số sao cho hàm số đồng biến trên A. 3. B. 4. C. 5. D. 2. Một vật chuyển động theo quy luật , với (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và (mét) là quảng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 12 giây, kể từ lúc bắt đầu chuyển động tại thời điểm bằng bao nhiêu giây thì vật đạt vận tốc lớn nhất ? A. . B. . C. . D. . Cho hàm số có đồ thị như hình sau: Đồ thị hàm số có số đường tiệm cận đứng là: A. 5. B. 3. C. 2. D. 1. Viết biểu thức về dạng và biểu thức về dạng. Ta có A. B. C. D. Cho hàm số có đồ thị như hình dưới: Hàm số có bao nhiêu điểm cực trị ? A.2. B.1. C.3. D.0. Cho hàm số . Xác định m để tiệm cận đứng của đồ thị hàm số đi qua điểm : A. B. C. D. Một chiếc bể inox có hình dạng khối lập phương có thể tích . Nếu tăng 3 kích thước(chiều dài, chiều rộng và chiều cao) của chiếc bể đó lên 3 lần thì chiếc bể đó sẽ chứa được nhiều nhất bao nhiêu lít nước? A. B. C. D. Cho hàm số có bảng biến thiên như hình dưới: Số điểm cực trị của hàm số là: A. 1. B. 2. C. 3. D. 5. Cho hàm số . Với giá trị nào của m thì đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số cùng hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 8. A. B. C. D. Cho hàm số có đồ thị như hình sau: Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. . B. . C. . D. . Có tất cả bao nhiêu giá trị nguyên của để hàm số nghịch biến trên khoảng ? A. B. C. Vô số D. Cho hàm số . Hàm số có đồ thị như hình bên. Hàm số có bao nhiêu điểm cực trị ? A. 2. B. 1. C. 0. D. 3. Biết tính giá trị của biểu thức : A. . B. . C. . D. . Một người thợ thủ công làm mô hình đèn lồng bát diện đều, mỗi cạnh của bát diện đó được làm từ các que tre có độ dài . Hỏi người đó cần bao nhiêu mét que tre để làm cái đèn (giả sử mối nối giữa các que tre có độ dài không đáng kể)? A. B. C. D. Số tiệm cận đứng của đồ thị hàm số là: A. 3 B. 0 C. 2 D. 1 Cho hàm số có đồ thị là đường cong như hình vẽ bên. Tìm tất cả các giá trị thực của để phương trình có 6 nghiệm phân biệt. A.. B. . C. D. . Cho hình chóp có đáy là tam giác vuông cân tại ; , . Cạnh bên hợp với đáy một góc . Thể tích của khối chóp tính theo bằng: A. . B. . C. . D. . Cho hàm số có bảng xét dấu như sau: Hàm số đồng biến trên khoảng nào? A.. B. . C. D. . Gọi là tập hợp các giá trị của để hàm số đạt giá trị lớn nhất bằng trên . Tổng các phần tử thuộc là A. . B. . C. . D. . Cho hình chóp có đáy là hình thang vuông tại A và D. Cạnh bên SA vuông góc với mặt phẳng đáy,, cạnh bên hợp với đáy một góc . Tính thể tích khối chóp theo a ? A. . B. . C. . D. . Cho hàm số có đồ thị của hàm số như sau: Trên khoảng có tất cả bao nhiêu số nguyên của để hàm số có đúng một cực trị ? A. 0. B. 14. C. 15. D. 13. -------------------Hết-------------------- Họ và tên:.................................................................Số báo danh.............................. Phòng thi......
Tài liệu đính kèm:
 de_kiem_tra_khao_sat_lan_1_mon_toan_lop_12_nam_hoc_2020_2021.docx
de_kiem_tra_khao_sat_lan_1_mon_toan_lop_12_nam_hoc_2020_2021.docx



