Đề kiểm tra học kì II môn Toán Lớp 12 - Năm học 2019-2020 - Trường THPT An Nghĩa - Mã đề 132
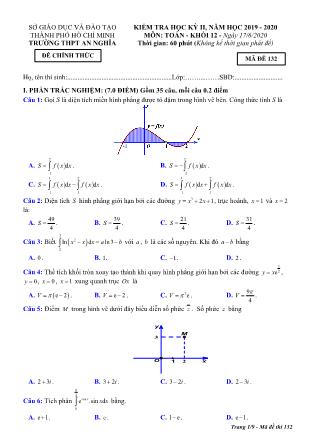
A. ( )
2 1
dS f x x=∫−
. B. ( )
2 1
dS f x x −
= −∫ .
C. ( ) ( )
1 2
1 1
S f x x f x x d d
−
= − ∫ ∫ . D. ( ) ( )
1 2
1 1
S f x x f x x d d
−
= + ∫ ∫ .
Câu 2: Diện tích S hình phẳng giới hạn bởi các đường y x x = + + 3 2 1, trục hoành, x =1 và x = 2
là:
A. 49
4
S = . B. 39
4
S = . C. 21
4
S = . D. 31
4
S = .
Câu 3: Biết ( )
3
2
2
∫ln d ln 3 x x x a b − = − với a , b là các số nguyên. Khi đó a b − bằng
A. 0 . B. 1. C. −1. D. 2 .
Câu 4: Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường e 2
x
y x = ,
y = 0, x = 0 , x =1 xung quanh trục Ox là
A. V = − π (e 2) . B. V = − e 2 . C. V = π 2e . D. 9
4
V = π .
Câu 5: Điểm M trong hình vẽ dưới đây biểu diễn số phức z . Số phức z bằng
A. 2 3 + i . B. 3 2 + i . C. 3 2 − i . D. 2 3 − i .
Câu 6: Tích phân
2
cos
0
e .sin d
π ∫
x
x x bằng.
A. e 1 + . B. e . C. 1 e − . D. e 1 − .
x
y
2
3
M
O 1
ĐỀ CHÍNH THỨC
MÃ ĐỀ 132Trang 2/9 - Mã đề thi 132
Câu 7: Trong không gian với hệ tọa độ Oxyz , cho điểm M (3; 1; 2 − − ) và mặt phẳng
(α ) : 3 2 4 0 x y z − + + = . Phương trình nào dưới đây là phương trình mặt phẳng đi qua M và song
song với (α)?
A. 3 2 6 0 x y z − − + = . B. 3 2 6 0 x y z − + − = .
C. 3 2 6 0 x y z − + + = . D. 3 2 14 0 x y z + − − = .
Câu 8: Cho M , N là các số thực, xét hàm số f x M x N x ( ) = + .sin π .cos π thỏa mãn f (1 3 ) = và
( )
12 0
1
d
π
∫ f x x = − . Giá trị của f ′ 14 bằng
A. π 2
2
. B. 5π 2
2
. C. π 2
2
− . D. 5π 2
2
− .
Câu 9: Cho hình phẳng giới hạn bởi các đường y x = −1, y = 0, x = 4 quay xung quanh trục Ox
. Thể tích khối tròn xoay tạo thành là
A. 5
6
V = π . B. 2
3
V = π . C. 7
6
V = π . D. 7
6
V = .
Câu 10: Trong không gian với hệ toạ độ Oxyz , cho hai điểm A(0;2;0) , B(−2;4;8) . Viết phương
trình mặt phẳng (α ) là mặt phẳng trung trực của đoạn AB .
A. (α ): 4 12 0 x y z − + − = . B. (α ): 4 12 0 x y z + − + = .
C. (α ): 4 20 0 x y z − − + = . D. (α ): 4 40 0 x y z − − + = .
Câu 11: Cho tích phân
2 0
I x x x 2 cos .sin d
π
= + ∫ . Nếu đặt t x = + 2 cos thì kết quả nào sau đây đúng?
A.
2 0
π dI t t=∫
. B.
3 2
I t t = ∫ d . C.
2 3
I t t = ∫ d . D.
2 3
I t t = 2 d ∫ .
Câu 12: Trong không gian với hệ tọa độ mặt phẳng qua cắt các trục tọa độ tại
điểm sao cho là trọng tâm tam giác có phương trình . Tính
.
A. 12 B. 9 C. 11 D. 10
Trang 1/9 - Mã đề thi 132 SỞ GIÁO DỤC VÀ ĐÀO TẠO THÀNH PHỐ HỒ CHÍ MINH TRƯỜNG THPT AN NGHĨA KIỂM TRA HỌC KỲ II, NĂM HỌC 2019 - 2020 MÔN: TOÁN - KHỐI 12 - Ngày 17/6/2020 Thời gian: 60 phút (Không kể thời gian phát đề) Họ, tên thí sinh:.............................................................Lớp: .... SBD:............................ I. PHẦN TRẮC NGHIỆM: (7.0 ĐIỂM) Gồm 35 câu, mỗi câu 0.2 điểm Câu 1: Gọi S là diện tích miền hình phẳng được tô đậm trong hình vẽ bên. Công thức tính S là A. ( ) 2 1 dS f x x − = ∫ . B. ( ) 2 1 dS f x x − = −∫ . C. ( ) ( ) 1 2 1 1 d dS f x x f x x − = −∫ ∫ . D. ( ) ( ) 1 2 1 1 d dS f x x f x x − = +∫ ∫ . Câu 2: Diện tích S hình phẳng giới hạn bởi các đường 3 2 1y x x= + + , trục hoành, 1x = và 2x = là: A. 49 4 S = . B. 39 4 S = . C. 21 4 S = . D. 31 4 S = . Câu 3: Biết ( ) 3 2 2 ln d ln 3x x x a b− = −∫ với a , b là các số nguyên. Khi đó a b− bằng A. 0 . B. 1. C. 1− . D. 2 . Câu 4: Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 2e x y x= , 0y = , 0x = , 1x = xung quanh trục Ox là A. ( )e 2V π= − . B. e 2V = − . C. 2eV π= . D. 9 4 V π= . Câu 5: Điểm M trong hình vẽ dưới đây biểu diễn số phức z . Số phức z bằng A. 2 3i+ . B. 3 2i+ . C. 3 2i− . D. 2 3i− . Câu 6: Tích phân 2 cos 0 e .sin d π ∫ x x x bằng. A. e 1+ . B. e . C. 1 e− . D. e 1− . x y 2 3 M O 1 ĐỀ CHÍNH THỨC MÃ ĐỀ 132 Trang 2/9 - Mã đề thi 132 Câu 7: Trong không gian với hệ tọa độ Oxyz , cho điểm ( )3; 1; 2M − − và mặt phẳng ( ) : 3 2 4 0x y zα − + + = . Phương trình nào dưới đây là phương trình mặt phẳng đi qua M và song song với ( )α ? A. 3 2 6 0x y z− − + = . B. 3 2 6 0x y z− + − = . C. 3 2 6 0x y z− + + = . D. 3 2 14 0x y z+ − − = . Câu 8: Cho M , N là các số thực, xét hàm số ( ) .sin π .cos πf x M x N x= + thỏa mãn ( )1 3f = và ( ) 1 2 0 1d π f x x = −∫ . Giá trị của 1 4 f ′ bằng A. π 2 2 . B. 5π 2 2 . C. π 2 2 − . D. 5π 2 2 − . Câu 9: Cho hình phẳng giới hạn bởi các đường 1y x= − , 0y = , 4x = quay xung quanh trục Ox . Thể tích khối tròn xoay tạo thành là A. 5 6 V π= . B. 2 3 V π= . C. 7 6 V π= . D. 7 6 V = . Câu 10: Trong không gian với hệ toạ độ Oxyz , cho hai điểm ( )0;2;0A , ( )2;4;8B − . Viết phương trình mặt phẳng ( )α là mặt phẳng trung trực của đoạn AB . A. ( ) : 4 12 0x y zα − + − = . B. ( ) : 4 12 0x y zα + − + = . C. ( ) : 4 20 0x y zα − − + = . D. ( ) : 4 40 0x y zα − − + = . Câu 11: Cho tích phân 2 0 2 cos .sin dI x x x π = +∫ . Nếu đặt 2 cost x= + thì kết quả nào sau đây đúng? A. 2 0 dI t t π = ∫ . B. 3 2 dI t t= ∫ . C. 2 3 dI t t= ∫ . D. 2 3 2 dI t t= ∫ . Câu 12: Trong không gian với hệ tọa độ mặt phẳng qua cắt các trục tọa độ tại điểm sao cho là trọng tâm tam giác có phương trình . Tính . A. 12 B. 9 C. 11 D. 10 Câu 13: Họ nguyên hàm của hàm số ( ) 5xf x = là: A. 15 1 x C x + + + . B. 5 ln 5 x C+ . C. 15x C+ + . D. 5 .ln 5x . Câu 14: Trong không gian Oxyz , cho mặt cầu ( ) 2 2 2: 4 2 6 5 0S x y z x y z+ + + − + + = . Mặt cầu ( )S có bán kính là A. 5 . B. 2 . C. 7 . D. 3 . Câu 15: Trên , phương trình 2 1 1 i z = + − có nghiệm là A. 2z i= − . B. 2z i= + . C. 1 2z i= − . D. 1 2z i= + . Câu 16: Trong không giam ,Oxyz mặt phẳng ( ) : 2 3 1 0P x y z+ + − = có một vectơ pháp tuyến là A. ( )2 1;3;2n −= . B. ( )1 2;3; 1n = − . C. ( )3 1;3;2n = . D. ( )4 2;3;1n = . ,Oxyz ( )1;2;3G , , A B C G ABC 18 0ax by cz+ + − = a b c+ + Trang 3/9 - Mã đề thi 132 Câu 17: Trong không gian Oxyz , cho điểm ( )1;0; 1M − . Mặt phẳng ( )α đi qua M và chứa trục Ox có phương trình là A. 0x z+ = . B. 1 0y z+ + = . C. 0x y z+ + = . D. 0y = . Câu 18: Tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn: 2 4z i+ − = là đường tròn có tâm I và bán kính R lần lượt là: A. ( )2; 1I − ; 4R = . B. ( )2; 1I − − ; 2R = . C. ( )2; 1I − ; 2R = . D. ( )2; 1I − − ; 4R = . Câu 19: Gọi 1z , 2z là hai nghiệm phức của phương trình 2 2 5 0z z− + = , trong đó 1z có phần ảo dương. Tìm số phức 2 21 22w z z= + . A. 9 4i+ . B. 9 4i− . C. 9 4i− − . D. 9 4i− + . Câu 20: Trong các mệnh đề sau, mệnh đề nào đúng? A. sin d cosx x x C= +∫ . B. dx xe x e C= +∫ . C. 1ln dx x C x = +∫ . D. 2 1 1dx C x x = − +∫ . Câu 21: Trong không gian với hệ tọa độ ,Oxyz cho hai điểm ( )3;0; 1A − , ( )5;0; 3 .B − Viết phương trình của mặt cầu ( )S đường kính .AB A. ( ) 2 2 2: 8 4 18 0S x y z x z+ + − + + = . B. ( ) ( ) ( )2 22: 2 2 4S x y z− + + + = . C. ( ) 2 2 2: 8 4 12 0.S x y z x z+ + − + + = D. ( ) ( ) ( )2 22: 4 2 8S x y z− + + + = . Câu 22: Tìm 6 2 d 3 1 x x x + −∫ . A. ( ) 2 4ln 3 1F x x x C= + − + B. ( ) ( )2 4ln 3 1F x x x C= + − + . C. ( ) 42 ln 3 1 3 F x x x C= + − + D. ( ) 4 ln 3 1 3 F x x C= − + Câu 23: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu ( )S có phương trình ( ) ( ) ( )2 2 24 3 1 9x y z+ + − + + = . Tọa độ tâm I của mặt cầu ( )S là ? A. ( )4; 3;1I − . B. ( )4;3;1I − . C. ( )4;3;1I . D. ( )4;3; 1I − − . Câu 24: Trong không gian Oxyz , phương trình của mặt phẳng ( )P đi qua điểm ( )2;1; 3B − , đồng thời vuông góc với hai mặt phẳng ( ) : 3 0Q x y z+ + = , ( ) : 2 0R x y z− + = là A. 4 5 3 22 0x y z+ − − = . B. 4 5 3 22 0x y z+ − + = . C. 2 3 14 0x y z+ − − = . D. 4 5 3 12 0x y z− − − = . Câu 25: Trong không gian Oxyz , cho mặt cầu ( ) ( ) ( ) ( )2 2 2: 1 3 2 49S x y z− + + + − = và điểm ( )7; 1;5M − . Phương trình mặt phẳng tiếp xúc với mặt cầu ( )S tại điểm M là. A. 6 2 3 55 0x y z+ + − = . B. 7 5 55 0x y z− + − = . C. 2 2 15 0x y z+ + − = . D. 6 2 2 34 0x y z− − − = . Câu 26: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( ) : 2 3 1 0P x y z+ + + = và điểm ( )1;2;0A . Khoảng cách từ A tới mặt phẳng ( )P bằng Trang 4/9 - Mã đề thi 132 A. 9 14 . B. 3 14 . C. 9 14 . D. 3 14 . Câu 27: Cho hai số phức 1 2 2z i= − , 2 3 3z i= − + . Khi đó số phức 1 2z z− là A. 1 i− + . B. 5 5i− + . C. 5i− . D. 5 5i− . Câu 28: Cho số phức z thỏa mãn ( )1 2 4 3 2i z i z+ = − + . Số phức liên hợp của số phức z là ? A. 2z i= − + . B. 2z i= − . C. 2z i= − − . D. 2z i= + . Câu 29: Trong không gian với hệ tọa độ ,Oxyz viết phương trình tham số của đường thẳng 4 3 2 : . 1 2 1 x y z− + − ∆ = = − . A. 1 4 : 2 3 1 2 x t y t z t = − ∆ = + = − − . B. 4 : 3 2 2 x t y t z t = − + ∆ = + = − − . C. 1 4 : 2 3 1 2 x t y t z t = + ∆ = − = − + . D. 4 : 3 2 2 x t y t z t = + ∆ = − + = − . Câu 30: Cho số phức ( ) ( )21 1 2z i i= + + . Số phức z có phần ảo là A. 4 . B. 4− . C. 2i . D. 2 . Câu 31: Cho số phức 1 1 3z i= + và 2 3 4z i= − . Môđun của số phức 1 2w z z= + là A. 15w = . B. 17w = . C. 15w = . D. 17w = . Câu 32: Trong không gian Oxyz , cho đường thẳng 1 1: 2 1 3 x y zd − −= = − − . Một vectơ chỉ phương của đường thẳng d là: A. ( )1 2; 1;3u = − . B. ( )3 2; 1; 3u = − − . C. ( )2 1;0;1u = . D. ( )4 2; 1;3u = − − . Câu 33: Nguyên hàm của hàm số ( ) sin 3f x x= là: A. cos3x C− + . B. 1 cos3 3 x C+ . C. 1 cos3 3 x C− + . D. cos3x C+ . Câu 34: Trong không gian ,Oxyz cho điểm 1; 1;3A và hai đường thẳng 1 4 2 1: 1 4 2 x y zd , 2 2 1 1 : . 1 1 1 x y zd Viết phương trình đường thẳng d đi qua điểm ,A vuông góc với đường thẳng 1d và cắt đường thẳng 2 .d A. 1 1 3: 2 1 3 x y zd . B. 1 1 3: 2 1 1 x y zd . C. 1 1 3: 4 1 4 x y zd . D. 1 1 3: 2 2 3 x y zd . Câu 35: Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm ( )1;2;2A , ( )5;4;4B và mặt phẳng ( ) : 2 6 0P x y z+ − + = Nếu M thay đổi thuộc ( )P thì giá trị nhỏ nhất của 2 2MA MB+ là A. 60 . B. 50 . C. 2968 25 . D. 200 3 . ----------------------------------------------- ----------- HẾT ---------- Trang 5/9 - Mã đề thi 132 SỞ GIÁO DỤC VÀ ĐÀO TẠO THÀNH PHỐ HỒ CHÍ MINH TRƯỜNG THPT AN NGHĨA KIỂM TRA HỌC KỲ II, NĂM HỌC 2019 - 2020 MÔN: TOÁN - KHỐI 12 - Ngày 17/6/2020 Thời gian: 30 phút (Không kể thời gian phát đề) Họ, tên thí sinh:.............................................................Lớp: .... SBD:............................ II. PHẦN TỰ LUẬN: ( 3,0 điểm ) Bài 1: (0,5 điểm) Cho hai số phức 1 1 2z i= + và 2 2 3z i= − . Tìm phần ảo của 1 23 2w z z= − . Bài 2: (0,5 điểm) Tìm số phức thỏa mãn: (2 ) 5 3 4 3z i i i− + − = + . Bài 3: (0,5 điểm) Trong không gian với hệ tọa độ Oxyz , cho hai điểm ( )1;1;2A , ( )2; 1;3B − . Viết phương trình đường thẳng AB . Bài 4: (0,5 điểm) Trong không gian với hệ trục toạ độ Oxyz , cho đường thẳng ( )d có phương trình là 2 1 8 3 5 x y z− + = = − . Viết phương trình mặt phẳng ( )P vuông góc với đường thẳng ( )d , biết ( )P đi qua điểm ( )0; 8;1M − . Bài 5: (0,5 điểm) Trong không gian Oxyz , cho đường thẳng ( ) 2 8 3: 1 3 2 x y z− − − ∆ = = và mặt phẳng ( ) :2 6 0P x y z+ − − = . Tìm tọa độ giao điểm của ( )∆ và ( )P . Bài 6: (0,5 điểm) Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng 1 1 2 : 2 1 1 x y zd − += = − và 2 1 2 2 : 1 3 2 x y zd − + −= = − . Gọi ∆ là đường thẳng song song với ( ) : 7 0P x y z+ + − = và cắt 1 2, d d lần lượt tại hai điểm ,A B sao cho AB ngắn nhất. Viết phương trình của đường thẳng ∆ . ---------- HẾT ---------- (Thí sinh không được sử dụng tài liệu) z ĐỀ CHÍNH THỨC Trang 6/9 - Mã đề thi 132 PHIẾU ĐÁP ÁN TRẮC NGHIỆM MÔN TOÁN 12 Mã đề: 132 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 A B C D Mã đề: 209 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 A B C D Mã đề: 357 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 A B C D Trang 7/9 - Mã đề thi 132 Mã đề: 485 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 A B C D Mã đề: 570 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 A B C D Mã đề: 628 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 A B C D 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 A B C D Trang 8/9 - Mã đề thi 132 ĐÁP ÁN TỰ LUẬN KIỂM TRA HKII KHỐI 12 NĂM HỌC 2019-2020 BÀI ĐÁP ÁN THANG ĐIỂM 1. Ta có 1 23 2w z z= − ( ) ( )3 1 2 2 2 3i i= + − − 1 12i= − + . Vậy phần ảo của số phức w là 12. 0,25 điểm 0,25 điểm 2. Ta có: 7 2 16 3 2 5 5 iz i i − = = + − 16 3 5 5 z i⇒ = − . 0,25 điểm 0,25 điểm 3. Ta có ( )1; 2;1AB = − . Đường thẳng AB đi qua điểm ( )1;1;2A và nhận véctơ ( )1; 2;1AB = − làm véctơ chỉ phương. Vậy phương trình của AB là 1 1 2 1 2 1 x y z− − − = = − . 0,25 điểm 0,25 điểm 4. ( ) ( )P d⊥ nên VTCP ( )8;3;5du = − của ( )d là một VTPT của ( )P . Khi đó ( ) ( ) ( ) qua 0; 8;1 : VTPT 8;3;5 M P n − = − ( ) : 8 3 5 19 0P x y z⇒ − + + + = ( ) :8 3 5 19 0P x y z⇔ − − − = . 0,25 điểm 0,25 điểm 5. Phương trình tham số của đường thẳng ( )∆ là: 2 8 3 3 2 = + = + = + x t y t z t với ∈ t . Tọa độ điểm M là nghiệm của hệ 2 8 3 3 2 2 6 0 = + = + = + + − − = x t y t z t x y z 1 1 5 1 = − =⇔ = = t x y z . Vậy ( )1;5;1M . 0,25 điểm 0,25 điểm 6. ( ) ( ) 1 2 1 2 ; ; 2 1 ; 2 3 ;2 2 A d A a a a B d B b b b ∈ ⇒ + − − ∈ ⇒ + − + − ∆ có vectơ chỉ phương ( )2 ;3 2; 2 4AB b a b a b a= − − − − + + Trang 9/9 - Mã đề thi 132 ( )P có vectơ pháp tuyến ( )1;1;1Pn = Vì ( )/ / P∆ nên . 0 1P PAB n AB n b a⊥ ⇔ = ⇔ = − .Khi đó ( )1;2 5;6AB a a a= − − − − ( ) ( ) ( )2 2 2 2 2 1 2 5 6 6 30 62 5 49 7 2 6 ; 2 2 2 AB a a a a a a a = − − + − + − = − + = − + ≥ ∀ ∈ Dấu " "= xảy ra khi 5 5 9 7 7 6; ; , ;0; 2 2 2 2 2 a A AB = ⇒ − = − Đường thẳng ∆ đi qua điểm 5 96; ; 2 2 A − và vec tơ chỉ phương ( )1;0;1du = − Vậy phương trình của ∆ là 6 5 2 9 2 x t y z t = − = = − + . 0,5 điểm
Tài liệu đính kèm:
 de_kiem_tra_hoc_ki_ii_mon_toan_lop_12_nam_hoc_2019_2020_truo.pdf
de_kiem_tra_hoc_ki_ii_mon_toan_lop_12_nam_hoc_2019_2020_truo.pdf



