1971 câu trắc nghiệm phần Hàm số môn Giải tích Lớp 12 (Phần 10)
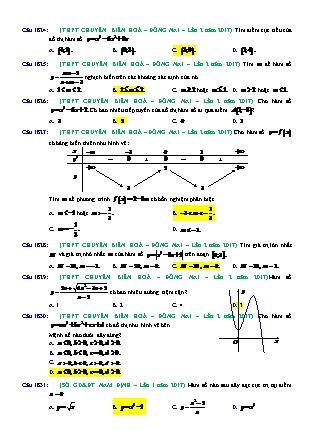
Câu 1830: (THPT CHUYÊN BIÊN HOÀ – ĐỒNG NAI – Lần 2 năm 2017) Cho hàm số có đồ thị như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Câu 1831: (SỞ GD&ĐT NAM ĐỊNH – Lần 1 năm 2017) Hàm số nào sau đây đạt cực trị tại điểm .
A. . B. . C. . D. .
Câu 1832: (SỞ GD&ĐT NAM ĐỊNH – Lần 1 năm 2017) Tìm tất cả các khoảng đồng biến của hàm số .
A. . B. . C. và .D.
Bạn đang xem tài liệu "1971 câu trắc nghiệm phần Hàm số môn Giải tích Lớp 12 (Phần 10)", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
(THPT CHUYÊN BIÊN HOÀ – ĐỒNG NAI – Lần 2 năm 2017) Tìm điểm cực tiểu của đồ thị hàm số . A. B. C. D. (THPT CHUYÊN BIÊN HOÀ – ĐỒNG NAI – Lần 2 năm 2017) Tìm để hàm số nghịch biến trên các khoảng xác định của nó. A. B. C. hoặc D. hoặc (THPT CHUYÊN BIÊN HOÀ – ĐỒNG NAI – Lần 2 năm 2017) Cho hàm số Có bao nhiêu tiếp tuyến của đồ thị hàm số đi qua điểm ? A. . B. . C. . D. . (THPT CHUYÊN BIÊN HOÀ – ĐỒNG NAI – Lần 2 năm 2017) Cho hàm số có bảng biến thiên như hình vẽ: Tìm để phương trình có bốn nghiệm phân biệt. A. hoặc B. C. D. (THPT CHUYÊN BIÊN HOÀ – ĐỒNG NAI – Lần 2 năm 2017) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn A. B. C. D. (THPT CHUYÊN BIÊN HOÀ – ĐỒNG NAI – Lần 2 năm 2017) Hàm số có bao nhiêu đường tiệm cận ? A. 1. B. 2. C. 4. D. 3. (THPT CHUYÊN BIÊN HOÀ – ĐỒNG NAI – Lần 2 năm 2017) Cho hàm số có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? A. B. C. D. (SỞ GD&ĐT NAM ĐỊNH – Lần 1 năm 2017) Hàm số nào sau đây đạt cực trị tại điểm . A.. B.. C.. D.. (SỞ GD&ĐT NAM ĐỊNH – Lần 1 năm 2017) Tìm tất cả các khoảng đồng biến của hàm số. A.. B.. C. và .D. (SỞ GD&ĐT NAM ĐỊNH – Lần 1 năm 2017) Tìm tiệm cận ngang của đồ thị hàm số . A.. B.. C.. D.. (SỞ GD&ĐT NAM ĐỊNH – Lần 1 năm 2017) Đồ thị hình bên là đồ thị của một trong 4 đồ thị của các hàm sốở các phương án A, B, C, D dưới đây. Hãy chọn phương án đúng. A.. B.. C.. D.. (SỞ GD&ĐT NAM ĐỊNH – Lần 1 năm 2017) Gọi , lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số trên đoạn . Tính giá trị của . A.. B.. C.. D.. (SỞ GD&ĐT NAM ĐỊNH – Lần 1 năm 2017) Cho hàm số có đồ thị .Tìm giá trị nhỏ nhất của tổng khoảng cách từ điểm thuộc tới hai đường thẳng và . A.. B.. C.. D.. (SỞ GD&ĐT NAM ĐỊNH – Lần 1 năm 2017) Gọi , lần lượt là số tiệm cận ngang, tiệm cận đứng của đồ thị hàm số . Mệnh đề nào sau đây đúng? A.. B.. C.. D.. (THPT QUỐC HỌC HUẾ - Lần 2 năm 2017)Cho hàm số có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau? A. . B. . C. . D. . (THPT QUỐC HỌC HUẾ - Lần 2 năm 2017) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên tập hợp . A. . B. . C. . D. . (THPT QUỐC HỌC HUẾ - Lần 2 năm 2017) Tìm số giao điểm của đồ thị hàm số và đường thẳng A. . B. . C. . D. . (THPT QUỐC HỌC HUẾ - Lần 2 năm 2017) Hàm số nghịch biến trên khoảng (hoặc các khoảng) nào sau đây? A. . B. và . C. và . D. . (THPT QUỐC HỌC HUẾ - Lần 2 năm 2017) Cho hàm số có đồ thị của nó trên khoảng như hình vẽ. Khi đó trên hàm số có bao nhiêu điểm cực trị? A. 1. B. 4. C. 3. D. 2. (THPT QUỐC HỌC HUẾ - Lần 2 năm 2017) Đồ thị hàm số có tất cả bao nhiêu đường tiệm cận? A. 3. B. 0. C. 2. D. 1. (THPT QUỐC HỌC HUẾ - Lần 2 năm 2017) Viết phương trình tiếp tuyến của tại giao điểm của với trục tung. A. . B. . C. . D. . (THPT QUỐC HỌC HUẾ - Lần 2 năm 2017) Cho hàm số có đạo hàm trên khoảng . Tìm mệnh đề sai trong các mệnh đề sau. A. Nếu hàm số đồng biến trên thì với mọi . B. Nếu với mọi thì hàm số nghịch biến trên . C. Nếu hàm số nghịch biến trên thì với mọi . D. Nếu với mọi thì hàm số đồng biến trên . (THPT QUỐC HỌC HUẾ - Lần 2 năm 2017)Cho hàm số có đạo hàm liên tục trên và đồ thị của hàm số trên đoạn như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau. A. . B. . C. . D. . (THPT QUỐC HỌC HUẾ - Lần 2 năm 2017) Gọi là giao điểm hai tiệm cận của đồ thị hàm số . Tìm tọa độ của A. . B. . C. . D. . (THPT QUỐC HỌC HUẾ - Lần 2 năm 2017) Cho hàm số có đồ thị trên như hình vẽ. Tìm . A. . B. . C. . D. . Cho hàm số có đạo hàm trên khoảng . Mệnh đề nào sau đây sai? A. Nếu đồng biến trên khoảng thì . B. Nếu thì hàm số đồng biến trên khoảng . C. Nếu không đổi trên khoảng thì . D. Nếu thì không đổi trên khoảng . Hỏi hàm số nghịch biến trên khoảng nào trong các khoảng sau đây? A. . B. . C. . D. . Hướng dẫn giải Cho hàm số liên tục trên và có bảng xét dấu như sau: Mệnh đề nào sau đây sai? A. Hàm số có đúng 2 điểm cực trị. B. Hàm số đạt cực đại tại . C. Hàm số đạt cực tiểu tại . D. Hàm số đạt cực tiểu tại . Tìm giá trị cực đại yCĐ của hàm số A. . B. . C. . D. . Tìm tất cả các giá trị của tham số thực để đồ thị hàm số có hai điểm cực trị đều nằm bên trái trục tung A. . B. . C. . D. . Đường thẳng nào dưới đây là đường tiệm cận ngang của đồ thị hàm số ? A. . B. . C. . D. . Hỏi đồ thị hàm số có bao nhiêu đường tiệm cận đứng ? A. 1. B. 2. C. 3. D. 4. Tìm giá trị lớn nhất của hàm số . A. . B. . C. . D. . Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình có đúng 2 nghiệm thực. A. . B. . C. . D. . Hỏi hai đồ thị và có bao nhiêu giao điểm ? A. . B. . C. . D. . (THPT CHUYÊN VÕ NGUYÊN GIÁP – QUẢNG BÌNH – Lần 1 năm 2017) Cho hàm số . Mệnh đề nào dưới đây đúng? A. Hàm số đồng biến trên khoảng . B. Hàm số nghịch biến trên khoảng . C. Hàm số đồng biến trên khoảng . D. Hàm số nghịch biến trên khoảng . (THPT CHUYÊN VÕ NGUYÊN GIÁP – QUẢNG BÌNH – Lần 1 năm 2017) Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số có phương trình lần lượt là: A. . B. . C. . D. . (THPT CHUYÊN VÕ NGUYÊN GIÁP – QUẢNG BÌNH – Lần 1 năm 2017)Cho hàm số xác định và liên tục trên đoạn và có đồ thị là đường cong ở hình vẽ bên. Mệnh đề nào dưới đây đúng trên đoạn . A. Hàm số đạt giá trị lớn nhất tại . B. Hàm số đạt cực đại tại . C. Hàm số đồng biến trên khoảng . D. Hàm số nghịch biến trên khoảng . (THPT CHUYÊN VÕ NGUYÊN GIÁP – QUẢNG BÌNH – Lần 1 năm 2017) Hàm số xác định và liên tục trên và có đạo hàm . Khi đó hàm số : A. Đạt cực đại tại điểm . B. Đạt cực tiểu tại điểm . C. Đạt cực đại tại điểm . D. Đạt cực tiểu tại điểm . (THPT CHUYÊN VÕ NGUYÊN GIÁP – QUẢNG BÌNH – Lần 1 năm 2017) Cho hàm số xác định, liên tục trên và có bảng biến thiên như sau: Tìm tập hợp tất cả các giá trị của tham số thực sao cho phương trình có ba nghiệm thực phân biệt. A. . B. . C. . D. . (THPT CHUYÊN VÕ NGUYÊN GIÁP – QUẢNG BÌNH – Lần 1 năm 2017) Bảng biến thiên dưới đây là của hàm số nào trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D sau: 1 + + A. . B. . C. . D. . (THPT CHUYÊN VÕ NGUYÊN GIÁP – QUẢNG BÌNH – Lần 1 năm 2017) Tìm tập hợp tất cả các giá trị của tham số thực để hàm số đồng biến trên từng khoảng xác định. A. . B. . C. . D. (THPT CHUYÊN VÕ NGUYÊN GIÁP – QUẢNG BÌNH – Lần 1 năm 2017) Biết hàm số đạt cực tiểu tại điểm , và đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng . Tính giá trị của hàm số tại . A. . B. . C. . D. . (THPT CHUYÊN VÕ NGUYÊN GIÁP – QUẢNG BÌNH – Lần 1 năm 2017) Biết các đường tiệm cận của đường cong cắt trục tạo thành một đa giác . Mệnh đề nào dưới đây đúng? A. là một hình vuông có diện tích bằng . B. là một hình chữ nhật có diện tích bằng . C. là một hình vuông có diện tích bằng . D. là một hình chữ nhật có diện tích bằng . (THPT CHUYÊN SƠN LA – Lần 2 năm 2017)Hàm số nào sau đây luôn nghịch biến trên từng khoảng xác định của nó? A. . B. . C. . D. . (THPT CHUYÊN SƠN LA – Lần 2 năm 2017)Cho hàm số có đồ thị là và đường thẳng Xác định tọa độ giao điểm của đường thẳng và đồ thị A. B. C. D. (THPT CHUYÊN SƠN LA – Lần 2 năm 2017)Cho hàm số liên tục trên và có bảng biến thiên như sau Hàm số đạt cực tiểu tại điểm nào sau đây ? A. B. C. D. (THPT CHUYÊN SƠN LA – Lần 2 năm 2017)Gọi là giá trị nhỏ nhất của hàm số trên đoạn . Vậy giá trị của là A. . B. . C. . D. . (THPT CHUYÊN SƠN LA – Lần 2 năm 2017)Cho hàm số có đồ thị là . Viết phương trình tiếp tuyến của tại điểm có hoành độ có phương trình A. . B. . C. . D. . (THPT CHUYÊN SƠN LA – Lần 2 năm 2017)Trong các hình vẽ sau, hình nào biểu diễn của đồ thị hàm số A. Hình 2. B. Hình 4. C. Hình 3. D. Hình 1. (THPT CHUYÊN SƠN LA – Lần 2 năm 2017)Tìm tất cả các giá trị của tham số để hàm số đạt cực trị tại . A. Không có giá trị nào của . B. . C. . D. hoặc . (THPT CHUYÊN SƠN LA – Lần 2 năm 2017)Hàm số nghịch biến trên khoảng nào ? A. . B. . C. . D. . (THPT CHUYÊN SƠN LA – Lần 2 năm 2017)Với giá trị nào của m thì hàm số đạt giá trị lớn nhất bằng trên . A. . B. . C. . D. . (THPT CHUYÊN SƠN LA – Lần 2 năm 2017)Cho hàm số tham số. Hỏi hàm số đã cho có thể có nhiều nhất bao nhiêu điểm cực trị? A. . B. . C. . D. . (THTT SỐ 478 – 2017) Hàm số có bao nhiêu điểm cực trị? A. . B. . C. . D. . (THTT SỐ 478 – 2017)Cho hàm số có đồ thị như hình vẽ dưới. Mệnh đề nào dưới đây đúng? A. . B. . C. . D. . (THTT SỐ 478 – 2017)Đồ thị hàm số tiếp xúc với đường thẳng tại bao nhiêu điểm? A. . B. . C. . D. . (THTT SỐ 478 – 2017)Cho hàm số Mệnh đề nào dưới đây đúng? A. Đồ thị hàm số đã cho có đúng một tiệm cận đứng. B. Đồ thị hàm số đã cho có đúng hai tiệm cận đứng. C. Đồ thị hàm số đã cho không có tiệm cận ngang. D. Đồ thị hàm số đã cho có đúng hai tiệm cận ngang. (THTT SỐ 478 – 2017)Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. B. C. D. (THTT SỐ 478 – 2017)Giả sử tồn tại hàm số xác định trên liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: Tập hợp tất cả các giá trị của tham số thực sao cho phương trình có bốn nghiệm thực phân biệt là A. B. C. D. (THTT SỐ 478 – 2017)Tập hợp tất cả các giá trị của tham số thực sao cho hàm số đạt cực đại tại là: A. . B. . C. . D. . (SỞ GD&ĐT THANH HOÁ – Lần 1 năm 2017) Cho hàm số . Mệnh đề nào dưới đây đúng? A. Hàm số nghịch biến trên các khoảng và . B. Hàm số nghịch biến trên các khoảng và . C. Hàm số đồng biến trên các khoảng và . D. Hàm số đồng biến trên các khoảng và . (SỞ GD&ĐT THANH HOÁ – Lần 1 năm 2017) Đồ thị của hàm số và đồ thị của hàm số có tất cả bao nhiêu điểm chung? A. . B. . C. . D. . (SỞ GD&ĐT THANH HOÁ – Lần 1 năm 2017)Cho hàm số liên tục trên và có đồ thị là đường cong như hình vẽ bên. Tìm điểm cực tiểu của đồ thị hàm số. A. B. C. D. (SỞ GD&ĐT THANH HOÁ – Lần 1 năm 2017) Cho hàm số liên tục trên đoạn và có đồ thị là đường cong như hình vẽ bên. Tìm số nghiệm của phương trình trên đoạn . A. . B. . C. . D. . (SỞ GD&ĐT THANH HOÁ – Lần 1 năm 2017) Gọi là hai điểm cực trị của hàm số . Tính giá trị của biểu thức . A. B. C. D. (SỞ GD&ĐT THANH HOÁ – Lần 1 năm 2017) Cho hàm số . Khẳng định nào dưới đây đúng? A. Đồ thị hàm số không có tiệm cận. B. Đồ thị hàm số có tiệm cận đứng là . C. Đồ thị hàm số có tiệm cận ngang là. D. Đồ thị hàm số có tiệm cận đứng là . (SỞ GD&ĐT THANH HOÁ – Lần 1 năm 2017) Một vật chuyển động theo quy luật , với (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu ? A. B. C. D. (SỞ GD&ĐT THANH HOÁ – Lần 1 năm 2017) Tìm số tiệm cận đứng của đồ thị hàm số A. . B. . C. . D. . (SỞ GD&ĐT THANH HOÁ – Lần 1 năm 2017) Cho hàm số có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? A. . B. . C. . D. . (THPT CHUYÊN LUONG THẾ VINH – ĐỒNG NAI – Lần 1 năm 2017) Hàm số liên tục trên và có bảng biến thiên dưới đây Khẳng định nào sau đây là đúng? A. Hàm số có ba điểm cực trị. B. Hàm số đạt cực đại tại . C. Hàm số đạt cực tiểu tại . D. Hàm số đạt cực đại tại . (THPT CHUYÊN LUONG THẾ VINH – ĐỒNG NAI – Lần 1 năm 2017) Cho hàm số . Khẳng định nào sau đây là đúng? A. Hàm số đồng biến trên khoảng . B. Hàm số đồng biến trên khoảng . C. Hàm số đồng biến trên khoảng . D. Hàm số nghịch biến trên khoảng . (THPT CHUYÊN LUONG THẾ VINH – ĐỒNG NAI – Lần 1 năm 2017) Số đường tiệm cận của đồ thị hàm số là: A. . B. . C. . D. (THPT CHUYÊN LUONG THẾ VINH – ĐỒNG NAI – Lần 1 năm 2017) Biết rằng đồ thị hàm số có hai điểm cực trị là và . Tính . A. B. C. D. (THPT CHUYÊN LUONG THẾ VINH – ĐỒNG NAI – Lần 1 năm 2017) Cho hàm số , . Khẳng định nào sau đây là sai? A. Hàm số luôn đơn điệu trên từng khoảng xác định. B. Đồ thị hàm số luôn có hai đường tiệm cận. C. Hàm số không có cực trị. D. Đồ thị hàm số luôn có tâm đối xứng. (THPT CHUYÊN LUONG THẾ VINH – ĐỒNG NAI – Lần 1 năm 2017) Cho hàm số liên tục trên đoạn và có đồ thị trên đoạn như hình bên. Khẳng định nào sau đây là sai? A. . B. . C. . D. . (THPT CHUYÊN LUONG THẾ VINH – ĐỒNG NAI – Lần 1 năm 2017) Cho hàm số . Khẳng định nào sau đây là đúng? A. Hàm số đạt cực tiểu tại . B. Hàm số có hai cực trị . C. Hàm số đạt cực đại tại . D. Giá trị cực tiểu bằng . (THPT CHUYÊN LUONG THẾ VINH – ĐỒNG NAI – Lần 1 năm 2017) Có bao nhiêu tham số nguyên để hàm số đồng biến trên ? A. B. Vô số. C. . D. . (THPT CHUYÊN LUONG THẾ VINH – ĐỒNG NAI – Lần 1 năm 2017) Cho hàm số có bảng biến thiên như sau: Khi đó có bốn nghiệm phân biệt khi và chỉ khi A. . B. . C. . D. . (THPT CHUYÊN LUONG THẾ VINH – ĐỒNG NAI – Lần 1 năm 2017) Các giá trị để đồ thị hàm số có đúng một đường tiệm cận đứng là A. . B. . C. . D. . (THPT QUẢNG XƯƠNG – THANH HOÁ – Lần 3 năm 2017) Cho hàm số xác định, liên tục trên có bảng biến thiên như hình dưới đây Khẳng định đúng là A. Hàm số nghịch biến trên khoảng . B. Hàm số có giá trị cực đại bằng . C. Hàm số đồng biến trên khoảng và . D. Hàm số có điểm cực tiểu là . (THPT QUẢNG XƯƠNG – THANH HOÁ – Lần 3 năm 2017)Tất cả các giá trị thực của tham số để hàm số nghịch biến trên nửa khoảng là: A. . B. . C. . D. . (THPT QUẢNG XƯƠNG – THANH HOÁ – Lần 3 năm 2017)Tất cả các giá trị thực của tham số để đồ thị hàm số có ba đường tiệm cận là A. . B. . C. . D. . (THPT QUẢNG XƯƠNG – THANH HOÁ – Lần 3 năm 2017)Cho hàm số có đồ thị . Khẳng định đúng là A. Đường thẳng là tiệm cận đứng của đồ thị . B. Đường thẳng là tiệm cận ngang của đồ thị . C. Đường thẳng là tiệm cận ngang của đồ thị . D. Đường thẳng là tiệm cận đứng của đồ thị . (THPT QUẢNG XƯƠNG – THANH HOÁ – Lần 3 năm 2017)Tổng tung độ các giao điểm của hai đồ thị hàm số và bằng A. . B. . C. . D. . (THPT QUẢNG XƯƠNG – THANH HOÁ – Lần 3 năm 2017)Khoảng đồng biến của hàm số là A. . B. . C. . D. . (THPT QUẢNG XƯƠNG – THANH HOÁ – Lần 3 năm 2017)Cho hàm số xác định và liên tục trên đoạn và có đồ thị là đường cong trong hình vẽ bên. Tất cả các giá trị thực của tham số m để phương trình có nghiệm phân biệt là A. . B. . C. . D. . (THPT QUẢNG XƯƠNG – THANH HOÁ – Lần 3 năm 2017)Tất cả các giá trị để đồ thị hàm số không cắt trục hoành là A. . B. . C. . D. . (THPT CHUYÊN KHTN – HÀ NỘI – Lần 2 năm 2017) Cho hàm số . Giá trị nhỏ nhất của hàm số bằng A. . B. . C. . D. . (THPT CHUYÊN KHTN – HÀ NỘI – Lần 2 năm 2017) Cho hàm số . Đồ thị hàm số có mấy tiệm cận? A. . B. . C. . D. . (THPT CHUYÊN KHTN – HÀ NỘI – Lần 2 năm 2017) Đồ thị hàm số nào sau đây không có tiệm cận ngang? A. . B. . C. . D. . (THPT CHUYÊN KHTN – HÀ NỘI – Lần 2 năm 2017) Cho hàm số . Tìm để hàm số đồng biến trên . A. . B. . C. . D. . (THPT CHUYÊN KHTN – HÀ NỘI – Lần 2 năm 2017) Khoảng cách giữa hai điểm cực trị của đồ thị hàm số bằng A. . B. . C. . D. . (THPT CHUYÊN KHTN – HÀ NỘI – Lần 2 năm 2017) Cho hàm số . Mệnh đề nào dưới đây đúng? A. Hàm số đồng biến trên khoảng và . B. Hàm số đồng biến trên khoảng . C. Hàm số đồng biến trên khoảng . D. Hàm số đồng biến trên khoảng . (THPT CHUYÊN KHTN – HÀ NỘI – Lần 2 năm 2017) Cho hàm số . Tiếp tuyến tại điểm có hoành độ bằng có hệ số góc bằng A. . B. . C. . D. . (THPT CHUYÊN KHTN – HÀ NỘI – Lần 1 năm 2017) Cho hàm số có đạo hàm là . Số điểm cực trị của hàm số là A. . B. . C. . D. . (THPT CHUYÊN KHTN – HÀ NỘI – Lần 1 năm 2017) Đường tiệm cận xiên của đồ thị hàm số tạo với hai trục tọa độ một tam giác có diện tích bằng A. . B. . C. . D. . (THPT CHUYÊN KHTN – HÀ NỘI – Lần 1 năm 2017) Hàm số: có giá trị cực đại và giá trị cực tiểu trái dấu khi A. hoặc . B. hoặc . C. . D. . (THPT CHUYÊN KHTN – HÀ NỘI – Lần 1 năm 2017) Đường thẳng nối hai điểm cực đại và cực tiểu của đồ thị hàm số đi qua điểm khi bằng A. . B. . C. . D. một giá trị khác. (THPT CHUYÊN KHTN – HÀ NỘI – Lần 1 năm 2017) Đường thẳng là tiếp tuyến của đường cong khi bằng A. . B. . C. . D. . (THPT CHUYÊN KHTN – HÀ NỘI – Lần 1 năm 2017) Cho hàm số . Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm khi bằng A. . B. . C. . D. . (THPT CHUYÊN KHTN – HÀ NỘI – Lần 1 năm 2017) Đồ thị hàm số có tâm đối xứng là điểm A. . B. . C. . D. . (THPT CHUYÊN KHTN – HÀ NỘI – Lần 1 năm 2017) Cho hàm số . Khẳng định nào dưới đây là khẳng định đúng. A. Hàm số đồng biến trên mỗi (từng) khoảng và . B. Hàm số nghịch biến trên mỗi (từng) khoảng và . C. Hàm số nghịch biến trên . D. Hàm số nghịch biến với mọi . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Cho hàm số có đồ thị như hình vẽ bên. Tiệm cận đứng của đồ thị hàm số là A. . B. . C. . D. . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Cho hàm số xác định, lên tục trên và có bảng biến. thiên sau. Khẳng định nào sau đây là đúng? A. Hàm số đồng biến trên khoảng . B. Hàm số có đúng một cực trị. C. Hàm số đạt cực đại tại và đạt cực tiểu tại . D. Hàm số có giá trị nhỏ nhất bằng và giá trị lớn nhất bằng . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Tọa độ điểm cực đại của đồ thị hàm số là A. . B. . C. . D. . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Giá trị lớn nhất của hàm số trên đoạn là A. . B. . C. . D. . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Tìm tất cả các giá trị của m để đồ thị hàm số cắt đường thẳng tại ba điểm phân biệt ? A. . B. . C. . D. . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Phương trình tiếp tuyến của đồ thị hàm số tại là A. . B. . C. . D. . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Tìm tất cả các giá trị của để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt có hoành độ dương? A. . B. . C. . D. . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Số đường tiệm cận của đồ thị hàm số là : A. . B. . C. . D. . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017)Cho hàm số có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? A. . B. . C. . D. . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Tìm tất cả các giá trị của tham số để đồ thị hàm số có đúng một cực trị. A. . B. . C. . D. . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Cho hàm số có đồ thị như hình vẽ bên. Tiệm cận đứng và tiệm cận ngang của đồ thị lần lượt là A. và . C. và . B. và . D. và . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Cho hàm số xác định, lên tục trên và có bảng biến thiên sau. Khẳng định nào sau đây là đúng? A. Hàm số đồng biến trên khoảng . B. Hàm số có đúng một cực trị. C. Hàm số đạt cực đại tại và đạt cực tiểu tại . D. Hàm số có giá trị nhỏ nhất bằng 0 và giá trị lớn nhất bằng 1. (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Đồ thị hàm số nào sau đây có 3 điểm cực trị? A. . B. . C. . D. . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Gọi và lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn . Khi đó tổng bằng: A. . B. . C. . D. . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Tìm tất cả các giá trị của để đồ thị hàm số cắt đường thẳng tại ba điểm phân biệt A. . B. . C. . D. . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Phương trình tiếp tuyến đồ thị hàm số tại là A. . B. . C. . D. . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Tìm tất cả các giá trị của để đường thẳng cắt đồ thị hàm số tại điểm phân biệt. A. B. C. D. (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Số tiệm cận ngang của đồ thị hàm số là A. B. C. D. (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017)Cho hàm số có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? A. . B. . C. . D. . (THPT HÀ HUY TẬP – HÀ TĨNH – Lần 2 năm 2017) Tìm tất cả các giá trị của tham số để đồ thị hàm số có đúng một cực tiểu. A. B. C. D. (THPT PHÚ XUYÊN A- HÀ NỘI – Lần 1 năm 2017) Hàm số đồng biến trên các khoảng A. . B. . C. . D. . (THPT PHÚ XUYÊN A- HÀ NỘI – Lần 1 năm 2017) Khoảng cách nhỏ nhất giữa hai điểm bất kỳ thuộc hai nhánh của đồ thị hàm số là A. . B. . C. . D. . (THPT PHÚ XUYÊN A- HÀ NỘI – Lần 1 năm 2017) Phương trình đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số lần lượt là A. và . B. và . C. và . D. và . (THPT PHÚ XUYÊN A- HÀ NỘI – Lần 1 năm 2017) Phương trình các đường tiệm cận ngang của đồ thị hàm số là. A. . B. . C. . D. và . (THPT PHÚ XUYÊN A- HÀ NỘI – Lần 1 năm 2017) Số giá trị của tham số để ba điểm cực trị của đồ thị hàm số là ba đỉnh của một tam giác vuông là A. . B. . C. . D. vô số. (THPT PHÚ XUYÊN A- HÀ NỘI – Lần 1 năm 2017) Đường cong trong hình bên là đồ thị của hàm số nào sau đây ? A. B. . C. . D. . (THPT PHÚ XUYÊN A- HÀ NỘI – Lần 1 năm 2017) Cho hàm số . Phương trình các đường tiếp tuyến của đồ thị hàm số tại giao điểm của nó với trục hoành là. A. và . B. và . C. và . D. và . (THPT PHÚ XUYÊN A- HÀ NỘI – Lần 1 năm 2017) Giá trị nhỏ nhất của hàm số với là. A. B. C. D. (THPT PHÚ XUYÊN A- HÀ NỘI – Lần 1 năm 2017) Cho hàm số . Hãy chọn đáp án đúng ? A. Hàm số nghịch biến trên và . B. Hàm số nghịch biến trên . C. Hàm số nghịch biến trên . D. Hàm số nghịch biến trên với . (THPT PHÚ XUYÊN A- HÀ NỘI – Lần 1 năm 2017) Cho hàm số: . Tất cả các giá trị của để hàm số luôn đồng biến trên là A. B. C. D. (THPT PHÚ XUYÊN A- HÀ NỘI – Lần 1 năm 2017) Cho hàm số điểm cực đại của hàm số là A. . B. . C. . D. hoặc . (THPT PHÚ XUYÊN A- HÀ NỘI – Lần 1 năm 2017) Cho hàm số , các giá trị thực của tham số để hàm số có hai điểm cực trị nằm về phía của trục tung là A. . B. . C. D. (SỞ GD&ĐT HẢI PHÒNG – Lần 2 năm 2017)Trong các hàm số sau, hàm số nào đồng biến trên khoảng ? A. . B. . C. . D. . (SỞ GD&ĐT HẢI PHÒNG – Lần 2 năm 2017)Đồ thị hình bên là của hàm số nào sau đây? A. . B. . C. . D. . (SỞ GD&ĐT HẢI PHÒNG – Lần 2 năm 2017)Tìm để hàm số nghịch biến trên A. . B. . C. . D. . (SỞ GD&ĐT HẢI PHÒNG – Lần 2 năm 2017)Cho hàm số có đồ thị Số tiếp tuyến với đồ thị mà song song với đường thẳng là A. . B. . C. . D. . (SỞ GD&ĐT HẢI PHÒNG – Lần 2 năm 2017)Đồ thị hàm số có tiệm cận đứng, tiệm cận ngang là A. Tiệm cận đứng: ; tiệm cận ngang: . B. Tiệm cận đứng: ; tiệm cận ngang: . C. Tiệm cận đứng: ; tiệm cận ngang: . D. Tiệm cận đứng: ; tiệm cận ngang: . (SỞ GD&ĐT HẢI PHÒNG – Lần 2 năm 2017)Giả sử hàm số có đạo hàm cấp một trên khoảng chứa điểm và có đạo hàm cấp hai tại điểm Mệnh đề nào sau đây là mệnh đề SAI? A. Nếu và thì là điểm cực trị của hàm số. B. Nếu và thì là điểm cực tiểu của hàm số. C. Nếu thì là điểm cực trị của hàm số. D. Nếu và thì là điểm cực đại của hàm số. (SỞ GD&ĐT HẢI PHÒNG – Lần 2 năm 2017)Cho hàm số Khẳng định nào sau đây là khẳng định SAI? A. Hàm số đồng biến trên các khoảng và . B. Đồ thị hàm số cắt trục tung tại điểm , cắt trục hoành tại điểm . C. Đồ thị hàm số đã cho không có điểm cực trị. D. Đồ thị hàm số có tiệm cận đứng là đường thẳng và tiệm cận ngang là đường thẳng (SỞ GD&ĐT HẢI PHÒNG – Lần 2 năm 2017)Cho hàm số . Gọi và lần lượt là hoành độ hai điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng? A. . B. . C. . D. . (SỞ GD&ĐT HẢI PHÒNG – Lần 2 năm 2017)Bảng biến thiên sau là của hàm số nào trong các hàm số cho dưới đây? A. . B. . C. . D. . (THPT CHUYÊN LÀO CAI – Lần 1 năm 2017) Giả sử hàm số có đạo hàm cấp hai trong khoảng , với . Khẳng định nào sau đây luôn đúng ? A. Nếu thì hàm số đạt cực đại tại B. Nếu và thì hàm số đạt cực đại tại C. Nếu và thì hàm số đạt cực đại tại D. Nếu và thì hàm số đạt cực tiểu tại (THPT CHUYÊN LÀO CAI – Lần 1 năm 2017) Đồ thị ở hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây? A. . B. . C. . D. . (THPT CHUYÊN LÀO CAI – Lần 1 năm 2017) Số đường tiệm cận của đồ thị hàm số là: A. . B. . C. . D. . (THPT CHUYÊN LÀO CAI – Lần 1 năm 2017)Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án dưới đây. Hỏi hàm số đó là hàm số nào?. A. . B. . C. . D. .
Tài liệu đính kèm:
 1971_cau_trac_nghiem_phan_ham_so_mon_giai_tich_lop_12_phan_1.doc
1971_cau_trac_nghiem_phan_ham_so_mon_giai_tich_lop_12_phan_1.doc



