Ôn tập môn Toán Lớp 12 - Chuyên đề ôn thi theo các mức điểm - Đối tượng học sinh khá mức 7-8 điểm (Có lời giải)

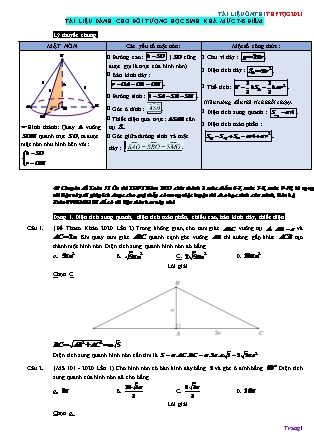
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ MỨC 7-8 ĐIỂM
Lý thuyết chung
MẶT NÓN
Các yếu tố mặt nón:
Một số công thức:
FHình thành: Quay vuông quanh trục , ta được mặt nón như hình bên với:.
§ Đường cao: . ( cũng được gọi là trục của hình nón).
§ Bán kính đáy: 
§ Đường sinh: 
§ Góc ở đỉnh: 
§ Thiết diện qua trục: cân tại 
§ Góc giữa đường sinh và mặt đáy: 
§ Chu vi đáy: 
§ Diện tích đáy: 
§ Thể tích: 
(liên tưởng đến thể tích khối chóp).
§ Diện tích xung quanh: 
§ Diện tích toàn phần: 
Dạng 1. Diện tích xung quanh, diện tích toàn phần, chiều cao, bán kính đáy, thiết diện
 (Đề Tham Khảo 2020 Lần 2) Trong không gian, cho tam giác vuông tại , và . Khi quay tam giác quanh cạnh góc vuông thì đường gấp khúc tạo thành một hình nón. Diện tích xung quanh hình nón đó bằng
A. .	B. .	C. .	D. .
Lời giải
Chọn C
.
Diện tích xung quanh hình nón cần tìm là .
 (Mã 101 - 2020 Lần 1) Cho hình nón có bán kính đáy bằng và góc ở đỉnh bằng . Diện tích xung quanh của hình nón đã cho bằng
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Gọi là đỉnh của hình nón và là một đường kính của đáy.
Theo bài ra, ta có tam giác là tam giác đều .
Vậy diện tích xung quanh của hình nón đã cho là .
 (Mã 102 - 2020 Lần 1) Cho hình nón có bán kính bằng 5 và góc ở đỉnh bằng . Diện tích xung quanh của hình nón đã cho bằng
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Ta có độ dài đường sinh là .
Diện tích xung quanh .
 (Mã 103 - 2020 Lần 1) Cho hình nón có bán kính bằng 3 và góc ở đỉnh bằng. Diện tích xung quanh của hình nón đã cho bằng
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Gọi là đường sinh, là bán kính đáy ta có .
Gọi là góc ở đỉnh. Ta có .
Vậy diện tích xung quanh .
 (Mã 104 - 2020 Lần 1) Cho hình nón có bán kính đáy bằng 4 và góc ở đỉnh bằng . Diện tích xung quanh của hình nón đã cho bằng
A. .	B. .	C. .	D. .
Lời giải
Chọn B
Ta có Góc ở đỉnh bằng .
Độ dài đường sinh: .
Diện tích xung quanh hình nón: .
 (Mã 123 2017) Cho một hình nón có chiều cao và bán kính đáy . Mặt phẳng đi qua cắt đường tròn đáy tại và sao cho . Tính khoảng cách từ tâm của đường tròn đáy đến .
A. 	B. 	C. 	D. 
Lời giải
Chọn C
Có .
Ta có , gọi là hình chiếu của lên suy ra là trung điểm , gọi là hình chiếu của lên suy ra .
Ta tính được suy ra là tam giác vuông cân tại , suy ra là trung điểm của nên 
 (KSCL THPT Nguyễn Khuyến 2019) Cho hình nón đỉnh , đường cao SO, và là hai điểm thuộc đường tròn đáy sao cho khoảng cách từ đến bằng và . Độ dài đường sinh của hình nón theo bằng
A. 	B. 	C. 	D. 
Lời giải
Chọn A
Gọi là trung điểm của ta có vì tam giác cân tại 
Mà nên mà nên từ dựng thì 
Xét tam giác ta có: 
Xét tam giác ta có: 
Xét tam giác ta có: 
 (THPT Cẩm Giàng 2 2019) Cho một hình nón có bán kính đáy bằng và góc ở đỉnh bằng . Tính diện tích xung quanh của hình nón đó.
A. .	B. .	C. .	D. .
Lời giải
Giả sử hình nón có đỉnh là , là tâm của đường tròn đáy và là một đường kính của đáy.
, .
Độ dài đường sinh là .
Vậy diện tích xung quanh của hình nón là .
 (THPT Cẩm Giàng 2 2019) Cho đoạn thẳng có độ dài bằng , vẽ tia về phía điểm sao cho điểm luôn cách tia một đoạn bằng . Gọi là hình chiếu của lên tia , khi tam giác quay quanh trục thì đường gấp khúc vẽ thành mặt tròn xoay có diện tích xung quanh bằng:
A. .	B. .	C. .	D. .
Lời giải
Xét tam giác vuông tại . Ta có 
Xét tam giác vuông tại , tại ta có 
Khi tam giác quay quanh trục thì đường gấp khúc vẽ thành mặt tròn xoay (có diện tích xung quanh là ) là hợp của hai mặt xung quanh của hình nón (N1) và (N2).
Trong đó:
(N1) là hình nón có được do quay tam giác quanh trục có diện tích xung quanh là 
(N2) là hình nón có được do quay tam giác quanh trục có diện tích xung quanh là 
.
 (HSG Bắc Ninh 2019) Cho hình nón có chiều cao , bán kính đáy . Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là . Tính diện tích của thiết diện đó.
A. 	B. 	C. 	D. 
Lời giải
Giả sử hình nón đỉnh , tâm đáy và có thiết diện qua đỉnh thỏa mãn yêu cầu bài toán là (hình vẽ).
Ta có là đường cao của hình nón. Gọi là trung điểm của .
Gọi là hình chiếu của lên .
Ta chứng minh được .
Xét tam giác vuông có .
.
Xét tam giác vuông có .
Xét tam giác vuông có .
Ta có .
 (Liên Trường THPT TP Vinh Nghệ An 2019) Cắt hình nón đỉnh cho trước bởi mặt phẳng qua trục của nó, ta được một tam giác vuông cân có cạnh huyền bằng Biết là một dây cung đường tròn của đáy hình nón sao cho mặt phẳng tạo với mặt phẳng đáy của hình nón một góc . Tính diện tích tam giác .
A. 	B. 	C. 	D. 
Lời giải
Thiết diện qua trục của hình nón là tam giác vuông cân, suy ra 
Ta có góc giữa mặt phẳng tạo với đáy bằng góc 
Trong tam giác vuông tại có và 
Mà 
Diện tích tam giác là 
 (Sở Hà Nội 2019) Cho hình nón tròn xoay có chiều cao bằng và bán kính bằng 3. Mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là một tam giác có độ dài cạnh đáy bằng . Diện tích của thiết diện bằng.
A. .	B. .	C. .	D. .
Lời giải
Ta có: .
Gọi M là trung điểm AB .
Lại có: ; .
Vậy: .
 (Chuyên Hạ Long 2019) Cắt hình nón bằng một mặt phẳng qua trục của nó, ta được một thiết diện là một tam giác vuông cân cạnh bên . Tính diện tích toàn phần của hình nón.
A. (đvdt).	B. (đvdt).	C. (đvdt).	D. (đvdt).
Lời giải
Giả sử hình nón đã cho có độ dài đường sinh , bán kính đáy là .
Thiết diện của hình nón qua trục là tam giác vuông cân tại O và .
Áp dụng định lý Pitago trong tam giác vuông cân ta có:
.
Vậy: .
Diện tích toàn phần của hình nón là:
 (đvdt).
 (Chuyên KHTN 2019) Cho hình lập phương cạnh . Tính diện tích toàn phần của vật tròn xoay thu được khi quay tam giác quanh trục .
A. .	B. .	C. .	D. .
Lời giải
Quay tam giác một vòng quanh trục tạo thành hình nón có chiều cao , bán kính đáy , đường sinh .
Diện tích toàn phần của hình nón: .
Cho hình nón có chiều cao và bán kính đáy đều bằng . Mặt phẳng qua đỉnh của hình nón và cắt đáy theo dây cung có độ dài bằng . Khoảng cách từ tâm của đáy tới mặt phẳng bằng
A. .	B. .	C. .	D. 
Lời giải
Chọn D
Ta có 
Mặt phẳng qua đỉnh của hình nón và cắt đáy theo dây cung có độ dài bằng ., là hình chiếu lên ; . Ta có 
ta có .
.
Cho hình nón đỉnh, đáy là đường tròn .Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm và sao cho . Tính khoảng cách từ đến .
A. .	B. .	C. .	D. .
Lời giải
Chọn B
Gọi là trung điểm .
Ta có .
Trong , kẻ thì .
.
Ta có: .
Ta có: .
Tam giác vuông có: .
Vậy .
 (Chuyên ĐHSPHN - 2018) Cho hình nón đỉnh , đáy là hình tròn tâm , bán kính, , góc ở đỉnh hình nón là . Cắt hình nón bởi mặt phẳng qua đỉnh tạo thành tam giác đều, trong đó , thuộc đường tròn đáy. Diện tích tam giác bằng
A. .	B. .	C. .	D. .
Lời giải
Theo đề bài ta có góc ở đỉnh hình nón là và khi cắt hình nón bởi mặt phẳng qua đỉnh tạo thành tam giác đều nên mặt phẳng không chứa trục của hình nón.
Do góc ở đỉnh hình nón là nên .
Xét tam giác vuông ta có .
Xét tam giác vuông ta có .
Do tam giác đều nên .
 (Chuyên Nguyễn Quang Diêu - Đồng Tháp - 2018) Cho hình nón có thiết diện qua trục là tam giác vuông có cạnh huyền bằng . Tính diện tích xung quanh của hình nón đó.
A. .	B. .	C. .	D. .
Lời giải
Gọi là đỉnh hình nón, thiết diện qua trục là tam giác .
Ta có , suy ra ; .
Vậy .