Ôn tập môn Toán Lớp 12 - Chuyên đề: Bài tập cực trị của hàm số
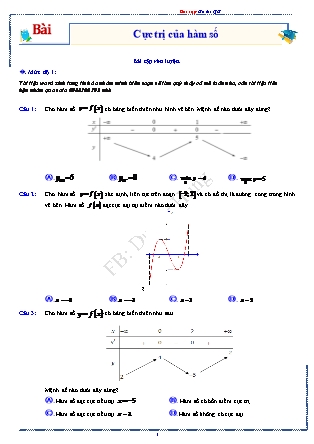
Câu 1: Cho hàm số có bảng biến thiên như hình vẽ bên. Mệnh đề nào dưới đây đúng?
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ.
Câu 2: Cho hàm số xác định, liên tục trên đoạn và có đồ thị là đường cong trong hình vẽ bên. Hàm số đạt cực đại tại điểm nào dưới đây
?
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ.
Câu 3: Cho hàm số có bảng biến thiên như sau
Bạn đang xem tài liệu "Ôn tập môn Toán Lớp 12 - Chuyên đề: Bài tập cực trị của hàm số", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Bài 2: Cực trị của hàm số Bài tập rèn luyện. ³. Mức độ 1: Cho hàm số có bảng biến thiên như hình vẽ bên. Mệnh đề nào dưới đây đúng? Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. Cho hàm số xác định, liên tục trên đoạn và có đồ thị là đường cong trong hình vẽ bên. Hàm số đạt cực đại tại điểm nào dưới đây ? Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. Cho hàm số có bảng biến thiên như sau Mệnh đề nào dưới đây đúng? Ⓐ. Hàm số đạt cực tiểu tại . Ⓑ. Hàm số có bốn điểm cực trị. Ⓒ. Hàm số đạt cực tiểu tại . Ⓓ. Hàm số không có cực đại Cho hàm số có bảng biến thiên như sau Hàm số đạt cực đại tại điểm Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Hàm số có bao nhiêu điểm cực trị? Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. Cho hàm số có bảng biến thiên như sau Tìm giá trị cực đại và giá trị cực tiểu của hàm số đã cho. Ⓐ. và . Ⓑ. và . Ⓒ. và . Ⓓ. và Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Cho hàm số (, , ) có đồ thị như hình vẽ bên Số điểm cực trị của hàm số đã cho là Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là: Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Cho hàm số có bảng biến thiên như sau. 0 0 Hàm số đã cho đạt cực tiểu tại. Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Cho hàm số có bảng biến thiên như sau: Hàm số đã cho đạt cực đại tại Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Cho hàm số có bảng biến thiên như sau: Hàm số đã cho đạt cực đại tại Ⓐ. Ⓑ. Ⓒ. Ⓓ. Cho hàm số có bảng biến thiên như sau: Hàm số đã cho đạt cực tiểu tại Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Cho hàm số có bảng biến thiên như sau Giá trị cực đại của hàm số đã cho bằng Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . ³. Mức độ 2: Tìm giá trị cực đại của hàm số . Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. Cho hàm số . Mệnh đề nào dưới đây đúng? Ⓐ.Cực tiểu của hàm số bằng . Ⓑ.Cực tiểu của hàm số bằng . Ⓒ. Cực tiểu của hàm số bằng . Ⓓ. Cực tiểu của hàm số bằng Cho hàm số có đạo hàm . Số điểm cực trị của hàm số đã cho là. Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Cho hàm số có đạo hàm . Số điểm cực trị của hàm số đã cho là Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Cho hàm số có đạo hàm ,. Số điểm cực trị của hàm số đã cho là Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Cho hàm số có đạo hàm , . Số điểm cực trị của hàm số đã cho là Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Cho hàm số có bảng biến thiên như sau Mệnh đề nào dưới đây sai Ⓐ.Hàm số có hai điểm cực tiểu. Ⓑ.Hàm số có giá trị cực đại bằng . Ⓒ. Hàm số có ba điểm cực trị. Ⓓ. Hàm số có giá trị cực đại bằng ³. Mức độ 3: Tìm tất cả các giá trị thực của tham số sao cho đồ thị của hàm số có ba điểm cực trị tạo thành một tam giác vuông cân Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Tìm tất cả các giá trị thực của tham số để hàm số không có cực đại? Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. Tìm tất cả các giá trị thực của tham số để đồ thị của hàm số có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn . Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. Đồ thị của hàm số có hai điểm cực trị và . Tính diện tích của tam giác với là gốc tọa độ. Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. Tìm giá trị thực của tham số để đường thẳng vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số Ⓐ. Ⓑ. Ⓒ. Ⓓ. Cho hàm số có bảng biến thiên như sau Đồ thị của hàm số có bao nhiêu điểm cực trị? Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. Tìm giá trị thực của tham số để hàm số đạt cực đại tại. Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. Có tất cả bao nhiêu giá trị nguyên của m để hàm số đạt cực tiểu tại Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. Vô số. Cho hàm số có đạo hàm , . Số điểm cực trị của hàm số đã cho là Ⓐ.. Ⓑ. Ⓒ. . Ⓓ. . Đồ thị hàm số có hai cực trị và . Điểm nào dưới đây thuộc đường thẳng ? Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Cho hàm số liên tục trên và có bảng xét dấu của như sau: Số điểm cực đại của hàm số đã cho là Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Cho hàm liên tục trên và có bảng xét dấu như sau: Số điểm cực tiểu của hàm số là Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Cho hàm số liên tục trên và có bảng xét dấu của như sau: Số điểm cực tiểu của hàm số đã cho là Ⓐ. Ⓑ. Ⓒ. Ⓓ. Cho hàm số liên tục trên R có bảng xét dấu Số điểm cực đại của hàm số đã cho là: Ⓐ.3. Ⓑ.1. Ⓒ. 2. Ⓓ. 4. Tìm tất cả các giá trị thực của tham số sao cho đồ thị của hàm số có ba điểm cực trị tạo thành một tam giác vuông cân Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Tìm tất cả các giá trị thực của tham số để hàm số không có cực đại? Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. Tìm tất cả các giá trị thực của tham số để đồ thị của hàm số có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn . Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. Đồ thị của hàm số có hai điểm cực trị và . Tính diện tích của tam giác với là gốc tọa độ. Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. Tìm giá trị thực của tham số để đường thẳng vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số Ⓐ. Ⓑ. Ⓒ. Ⓓ. Cho hàm số có bảng biến thiên như sau Đồ thị của hàm số có bao nhiêu điểm cực trị? Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . Tìm giá trị thực của tham số để hàm số đạt cực đại tại. Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. Có tất cả bao nhiêu giá trị nguyên của m để hàm số đạt cực tiểu tại Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. Vô số. Cho hàm số có đạo hàm , . Số điểm cực trị của hàm số đã cho là Ⓐ.. Ⓑ. Ⓒ. . Ⓓ. . Đồ thị hàm số có hai cực trị và . Điểm nào dưới đây thuộc đường thẳng ? Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. BẢNG ĐÁP ÁN 1.A 2.B 3.C 4.D 5.B 6.A 7.A 8.D 9.B 10.D 11.C 12.C 13.D 14.C 15.D 16.A 17.D 18.D 19.B 20.C 21.A 22.B 23.B 24.A 25.C 26.D 27.B 28.B 29.C 30.C 31.B 32.C 33.C 34.B 35 36.C 37.B 38.A 39.C 40.D 41.B 42.B 43.C 44.C 45.B 46.C
Tài liệu đính kèm:
 on_tap_mon_toan_lop_12_chuyen_de_bai_tap_cuc_tri_cua_ham_so.docx
on_tap_mon_toan_lop_12_chuyen_de_bai_tap_cuc_tri_cua_ham_so.docx



