Đề cương ôn tập học kỳ I môn Hình học Lớp 12

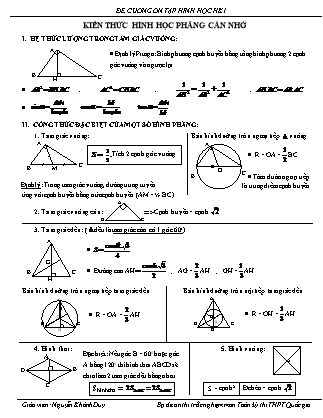
KIẾN THỨC HÌNH HỌC PHẲNG CẦN NHỚ 
Định lý Pitago: Bình phương cạnh huyền bằng tổng bình phương 2 cạnh góc vuông và ngược lại
B
A
C
H
HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG:
	; 	 	; 	; 
II. CÔNG THỨC ĐẶC BIỆT CỦA MỘT SỐ HÌNH PHẲNG:
O
 Tích 2 cạnh góc vuông
 R = OA =BC
Tâm đtròn ngoại tiếp là trung điểm cạnh huyền 
A
B
A
C
I
M
Tam giác vuông: 	 Bán kính đường tròn ngoại tiếp vuông	
R
C
B
I
Định lý: Trong tam giác vuông, đường trung tuyến
 ứng với cạnh huyền bằng nửa cạnh huyền. (AM = ½ BC )
A
C
B
Tam giác vuông cân: => Cạnh huyền = cạnh.
 Đường cao AH ; AG =AH ; GH =AH 
H
A
B
C
G
Tam giác đều: (đều là tam giác cân có 1 góc 600)
H
A
B
C
O
O
 R = OH =AH 
H
A
B
C
O
 R = OA =AH 
H
A
B
C
O
Bán kính đường tròn ngoại tiếp tam giác đều	
 R = OA =AH 
	 Bán kính đường tròn nội tiếp tam giác đều
R
R
Đặc biệt: Nếu góc B = 600 hoặc góc A bằng 1200 thì hình thoi ABCD sẽ chia làm 2 tam giác đều bằng nhau
A
B
C
D
Hình thoi:	 5. Hình vuông:
Shìnhthoi = =
Đchéo = cạnh. 
S = cạnh 2
 R = OI =cạnh
R
D
A
B
C
A
B
C
D
O
R
O
A
B
C
D
R
 R = OA =đường chéo
Bán kính đường tròn ngoại tiếp hình vuông / hình chữ nhật	A
B
C
D
O
R
O
A
B
C
D
R
 Bán kính đtròn nội tiếp hình vuông	
I
O
 A
B
C
 D
đáy lớn
A
B
C
D
đáy bé
đcao
6. Hình thang:	 	 (Hình thang vuông)
III. MỘT VÀI CHỨNG MINH THÔNG DỤNG:
MN // BC
Chứng minh 2 tam giác bằng nhau: Thường gặp: C – G – C , nếu 2 tam giác vuông thì thường CM 2 tam giác bằng nhau theo 2 cách: cạnh huyền – góc nhọn; cạnh huyền – cạnh góc vuông
A
B
C
N
M
Định lý Ta – lét:
3. Đường trung bình: Nếu M, N trung điểm AB, AC thì MN // BC và MN = ½ BC
I
Chứng minh 2 tam giác vuông đồng dạng:
H
D
A
B
C
K
	 VD: Xét 2 tam giác vuông ADI và HKD: A = K = 900, D chung	
K
Shình tròn = , r là bán kính
SABC = ..
SABC = , với
IV. MỘT VÀI CÔNG THỨC TÍNH CHU VI, S, R, r THÔNG DỤNG:
 	CHU VI	 	 DIỆN TÍCH
 ĐN: Là độ dài đường biên bao quanh
 (giới hạn) hình phẳng đó .
Chu vi tam giác = tổng độ dài 3 cạnh 
Chu vi hình chữ nhật = (dài + rộng) x 2
Chu vi đtròn =, với r là bán kính
B
A
 VD: Cho đoạn thẳng AB = 10cm
Uốn đoạn thẳng AB thành 1 đường tròn thì chu vi đường tròn cũng bằng độ dài AB = 10cm
MỘT SỐ KIẾN THỨC VỀ KHỐI ĐA DIỆN
Loại { p ; q } :
p : Mỗi mặt của nó là đa giác đều p cạnh
q: Mỗi đỉnh của nó là đỉnh chung của q mặt
 Bảng tóm tắt 5 loại khối đa diện đều:
Loại
Tên gọi
Số đỉnh
Số cạnh
Số mặt phẳng đối xứng
{3;3}
Tứ diện đều
4
6
6
{4;3}
Lập phương
8
12
9
{3;4}
Bát diện đều
6
12
9
{5;3}
12 mặt đều
20
30
{3;5}
20 mặt đều
12
30
Một số ví dụ minh họa về hình đa diện và hình không phải hình đa diện:
 Hình đa diện:
 Hình không phải là hình đa diện:
 Một số ví dụ về mặt phẳng đối xứng của hình đa diện:
Hình hộp chữ nhật có 3 kích thước khác nhau: 3 mặt phẳng đối xứng
Hình hộp đứng đáy hình thoi: 3 mặt phẳng đối xứng
Hình lăng trụ tam giác đều: 4 mặt phẳng đối xứng
 Phân chia và lắp ghép khối đa diện, khối đa diện trong khối đa diện:
VD: Mặt phẳng (AB’C’) chia khối lăng trụ ABC.A’B’C’ thành các khối đa diện nào?
Một khối chóp tam giác và một khối chóp tứ giác
Hai khối chóp tam giác
Một khối chóp tam giác và một khối chóp tứ giác
Hai khối chóp tứ giác
CÁC DẠNG TOÁN QUAN HỆ VUÔNG GÓC TRONG HHKG
Dạng 1: Chứng minh đường thẳng vuông góc mặt phẳng:
 Chứng minh đường thẳng đó vuông góc với 2 đường cắt nhau nằm trong mp.
Tính chất: Nếu đường thẳng vuông góc mặt phẳng thì nó vuông góc với mọi đường nằm trong mp đó
Dạng 2: Chứng minh hai mp vuông góc (áp dụng tính khoảng cách):
Ta chứng minh mặt phẳng này chứa một đường thẳng vuông góc mặt phẳng kia. 
Dạng 3: Cách xác định góc giữa đường thẳng và mặt phẳng:
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng. 
Dạng 4: Cách xác định góc giữa 2 mặt phẳngvà :
Xác định giao tuyến d 
Trong tìm đường thẳng ad, trong tìm đường thẳng b d sao cho a cắt b.
M
d
H
	 Góc giữa và là góc giữa a và b
Dạng 5: Tính khoảng cách từ điểm M đến mặt phẳng:
Phương pháp: Dựng mp . Khi đó sẽ có 2 tình huống :
TH1: M: Kẻ MH với giao tuyến d của và
 Khoảng cách là MH 
TH2: M: Quy về tỉ lệ khoảng cách (sẽ nói rõ hơn trong phần bài tập)
Dạng 6: Khoảng cách giữa 2 đường thẳng chéo nhau:
a
TH1: Đường thẳng này vuông góc mp chứa đường thẳng kia
b
Giả sử đường thẳng a vuông góc mp chứa đường thẳng b. Đthẳng a cắt tại M. Khi đó kẻ MH b (a, b) = MH
M
H
TH2: Trường hợp tổng quát với 2 đường thẳng a, b chéo nhau:
Bước 1: Tìm mp chứa b sao cho a //
Bước 2: (a, b) = (M,), với Ma 
(Đem về bài toán tính khoảng cách từ điểm đến mặt phẳng của Dạng 5)
M
a
b
H
MỘT VÀI HÌNH KHÔNG GIAN THÔNG DỤNG
Tính chất hình chóp đều:
Đáy là đều hoặc h.vuông
SO(đáy)
SA = SB = SC = SD
H
 C
 O
 B
D
 A
H
 B
O
 A
C
 S
C
B
A
D
O
S
Hchóp đều: (Tứ diện đều là hình chópđều có tất cả các cạnh bằng nhau)
Hình chóp tam giác đều	 Tứ diện đều ABCD 	 Hình chóp tứ giác đều (đáy hình vuông)
B’
C
A’
C’
A
B
C
 C’
A’
A
B’
H
B
A’
B’
C’
A
B
C
Hình lăng trụ (nếu không nói lăng trụ đứng hoặc đều thì nó sẽ vẽ nghiêng):
D’
D
Lăng trụ đứng ABC.A’B’C’
Lăng trụ ABC.A’B’C’, hình chiếu của A’ trùng với tr.điểm cạnh AB
(Từ H vẽ thẳng đứng lấy điểm A’)
Lăng trụ tứ giác đều ABCD.A’B’C’D’
là hình hộp chữ nhật có đáy là hvuông
Lăng trụ đều (lăng trụ tam giác đều, tứ giác đều) là lăng trụ đứng, có đáy là đều hoặc hình vuông...
O
A
B
C
S
C
B
A
D
 Đường cao mặt bên mặt đáy
Hình chóp có mặt bên mặt đáy:
H
A
Tứ diện OABC có 3 cạnh 
OA, OB, OC đôi một vuông góc
Hchóp S.ABCD, mặt bên (SAD) (ABCD) 
vàSAD đều (hoặc cân tại S) SH (ABCD)
Bát diện đều
O
MẶT NÓN, MẶT TRỤ
S
A
B
Khoảng cách từ O đến mp(SAB) là OH
 Hình nón tròn xoay:
h
Cho D OIM vuông tại I. Khi quay nó xung quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình được gọi là hình nón tròn xoay.
l
Thiết diện (mp) qua đỉnh: SAB
R
 OI: đường cao h ; IM: Bán kính R ; OM: đường sinh l	 Thiết diện qua trục: SAB
 Hình trụ tròn xoay:
Xét hình chữ nhật ABCD. Khi quay hình đó xung quanh đường thẳng chứa 1 cạnh, chẳng hạn AB, thì đường gấp khúc ADCB tạo thành một hình gọi là hình trụ tròn xoay.
B
A
l
h
R
D
C
 Trong đó: h = l = AB = CD ; Bán kính R = BC = AD 	 Thiết diện qua trục: H.chữ nhật ABCD
XÁC ĐỊNH TÂM VÀ BÁN KÍNH MẶT CẦU NGOẠI TIẾP KHỐI ĐA DIỆN
ĐỊNH NGHĨA: Mặt cầu ngoại tiếp hình chóp là mặt cầu đi qua các đỉnh của hình chóp.
	Ví dụ: Nếu mặt cầu ngoại tiếp hình chóp S.ABCD có tâm là điểm I thì R = IA = IB = IC = ID = IS
CÁCH XÁC ĐỊNH TÂM MẶT CẦU NGOẠI TIẾP HÌNH CHÓP THƯỜNG GẶP
Bước 1: Xác định tâm O của đường tròn ngoại tiếp đa giác đáy. (Xem Kiến thức cần nhớ bên dưới)
Bước 2: Từ O kẻ đường thẳng d vuông góc mp đáy (d là trục đường tròn ngoại tiếp của đa giác đáy)
Bước 3: Xác định đường trung trực l của một cạnh bên hoặc trục đường tròn ngoại tiếp mặt bên. Khi đó giao điểm I của l và d chính là tâm mặt cầu ngoại tiếp cần tìm. (Xem các Ví dụ minh họa bên dưới)
Tâm đường ngoại tiếp của đều là trọng tâm, của vuông là trung điểm cạnh huyền, của hình vuông hoặc hình chữ nhật là giao điểm 2 đường chéo (Xem lại Kiến thức hình học phẳng cần nhớ )
Đường trung trực của đoạn thẳng là đường thẳng vuông góc tại trung điểm của đoạn thẳng ấy.
 C
 B
 A
 S
 I
O
I
C
O
Ví dụ minh họa: HÌNH CHÓP CÓ CẠNH BÊN VUÔNG GÓC ĐÁY:
Hình chóp S.ABC có đáy tam giác ABC vuông tại A. Tính R bằng cách dựng hình chữ nhật OIMA
Hình chóp S.ABC có đáy tam giác đều ABC. Tính R bằng cách dựng hình chữ nhật OIMA
M
I
O
C
 B
 A
 S
l
I
O
C
B
A
S
M
l
, với
l
C
B
A
D
O
S
I
M
l
C
 B
 A
 S
HÌNH CHÓP ĐỀU, 	TỨ DIỆN ĐỀU
R =
I
O
O’
I
C
B
D
S
H
O
 A
MẶT CẦU NGOẠI TIẾP HÌNH CHÓP CÓ MẶT BÊN VUÔNG GÓC MẶT ĐÁY
Cho hình chóp S.ABCD, đáy hình vuông hoặc hình chữ nhật có mặt bên với đáy (Giả sử mp (SAB)đáy), và SAB đều
Xác định tâm O của hình vuông ABCD
Từ O kẻ đường thẳng vuông góc với đáy
Xác định tâm đtròn ngoại tiếp O’ của mp (SAB)
Dựng hình chữ nhật OIO’H R = SI
Cách dựng:
 R = SI , với 
MẶT CẦU NGOẠI TIẾP HÌNH HỘP CHỮ NHẬT, HÌNH LẬP PHƯƠNG
 A’
B’
A
B
C
D
C’
I
Tâm mặt cầu là trung điểm I của đường chéo hình hộp
 R = 
Đối với Đối với hình lập phương: R = 
( Đường chéo hình lập phương = cạnh	
TỔNG HỢP CÔNG THỨC VỀ KHỐI ĐA DIỆN, KHỐI TRÒN XOAY, MẶT CẦU
Hình
Công thức
Hình chóp
Hình lăng trụ
Hình nón
Hình trụ
Mặt cầu
Diện tích
 xung quanh
Tổng diện tích các mặt bên
Tổng diện tích các mặt bên
Diện tích
 Toàn phần
Tổng diện tích các mặt bên và mặt đáy
Tổng diện tích các mặt bên và mặt đáy
( Sđáy : )
( Sđáy : )
Thể tích
TỔNG HỢP CÁC CÔNG THỨC ĐẶC BIỆT KHÁC
Thể tích khối tứ diện đều: 	 Ø Thể tích khối bát diện đều: 
Trong hình lập phương: Thể tích: V = cạnh 3 Đường chéo = cạnh .
(dài, rộng, cao)
Trong hình hộp chữ nhật có 3 kích thước a, b, c: Thể tích: V = a.b.c Đường chéo = 
C
B
 B’
A’
A
C’
Ví dụ: Cho hình lăng trụ ABC.A’B’C’ có thể tích V . Khi đó:
VA’B’CC’ = VA’ABC’ = VA’B’CB = = V
VA’B’C’CB = VCBAA’B’ = VBACC’A’ = V
Trong hình lăng trụ tam giác có thể tích V:
Vtứ diện (tạo bởi 4 điểm tùy ý) =V
Vhình chóp (tạo bởi 5 điểm tùy ý) =V
Ví dụ: Cho hhộp ABCD.A’B’C’D’ có thể tích V . Khi đó:
VCC’D’A = VBB’C’D = = V
VB’D’CA = VA’C’BD = = V
 A’
B’
A
B
C
D
C’
D’
Trong hình hộp có thể tích V:
Vtứ diện (3 trong 4 đỉnh nằm trên 1 mặt hình hộp ) =V
Vtứ diện (4 điểm tùy ý không phải dạng như trên) =V
TỈ SỐ THỂ TÍCH 
Lưu ý: A’ có thể trùng A
 	 B’ có thể trùng B...