Giáo án Giải tích Lớp 12 - Chương II, Bài 2: Hàm số lũy thừa

Chủ đề 1. HÀM SỐ LŨY THỪA
Thời lượng dự kiến: 02 tiết
I. MỤC TIÊU
1. Kiến thức
- Hiểu định nghĩa của hàm số lũy thừa, công thức tính đạo hàm của hàm số lũy thừa
- Nắm được cách vẽ đồ thị hàm số lũy thừa
2. Kĩ năng
- Biết tính đạo hàm của hàm số lũy thừa và vẽ đồ thị hàm số lũy thừa.
- Biết tìm tập xác định của hàm số lũy thừa tùy thuộc vào điều kiện của lũy thừa.
3.Về tư duy, thái độ	
- Chủ động phát hiện, chiếm lĩnh tri thức mới, biết quy lạ về quen, có tinh thần hợp tác xây dựng cao.
4. Định hướng các năng lực có thể hình thành và phát triển: Năng lực tự học, năng lực giải quyết vấn đề, năng lực tự quản lý, năng lực giao tiếp, năng lực hợp tác, năng lực sử dụng ngôn ngữ. 
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH
1. Giáo viên
+ Giáo án, phiếu học tập, phấn, thước kẻ, máy chiếu, ...
2. Học sinh
+ Đọc trước bài
+ Chuẩn bị bảng phụ, bút viết bảng, khăn lau bảng 
III. TIẾN TRÌNH DẠY HỌC
HOẠT ĐỘNG KHỞI ĐỘNG
A
Mục tiêu: Tiếp cận khái niệm hàm số lũy thừa
Nội dung, phương thức tổ chức hoạt động học tập của học sinh
Dự kiến sản phẩm, đánh giá kết quả hoạt động
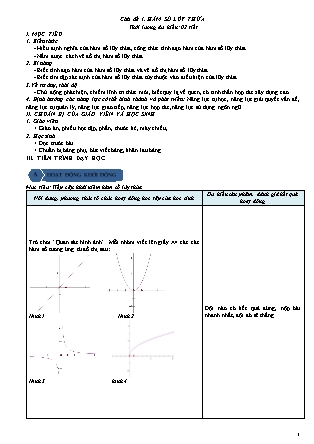
Trò chơi “Quan sát hình ảnh”. Mỗi nhóm viết lên giấy A4 các các hàm số tương ứng từ đồ thị sau: 
Hình 1 Hình 2
Hình 3 hình 4
Đội nào có kết quả đúng, nộp bài nhanh nhất, đội đó sẽ thắng
HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
B
Mục tiêu: Nắm được định nghĩa hàm số lũy thừa.
Nội dung, phương thức tổ chức hoạt động học tập của học sinh
Dự kiến sản phẩm, đánh giá kết quả hoạt động
I. KHÁI NIỆM HÀM SỐ LŨY THỪA
Hàm số với a Î R được gọi là hàm số luỹ thừa.
Chú ý: Tập xác định của hàm số tuỳ thuộc vào giá trị của a:
· a nguyên dương: D = R
· : D = R \ {0}
· a không nguyên: D = (0;+∞)
Ví dụ 1. Hoàn thành phiếu học tập số 1
Phương thức tổ chức: Theo nhóm – tại lớp.
* Hoàn thành chính xác phiếu học tập số 1, từ đó rút ra nhận xét mối liên hệ giữa tập xác định của hàm số với số mũ lũy thừa.
VD2: Tìm tập xác định của các hàm số:
a) 
b) 
c) 
d) 
Phương thức tổ chức: Cá nhân – tại lớp.
KQ1. 
a) 1 – x > 0 Þ D = (–∞; 1)
b) 
	Þ D = 
c) 
	Þ D = R \ {–1; 1}
d) 
 Þ D = (–∞; –1) È (2; +∞)
II. ĐẠO HÀM CỦA HÀM SỐ LUỸ THỪA
 1. công thức tính đạo hàm của hàm số lũy thừa
 (x > 0)
VD3: Tính đạo hàm của các hàm số sau
a) 	b) 
c) 	d) 
Phương thức tổ chức: Cá nhân – tại lớp.
*Đọc hiểu công thức tính đạo hàm của hàm số lũy thừa.
KQ2
a) b) 
c) d) 
2. Áp dụng
VD4: VD2: Tính đạo hàm:
a) 
b) 
c) 
d) 
Phương thức tổ chức: Cá nhân – tại lớp.
*Thực hiện vào tập, bạn nào thực hiện nhanh và chính xác nhất lên bảng thực hiện từng câu.
a) 
b) 
c) 
d) 
III.KHẢO SÁT HÀM SỐ LŨY THỪA.
(a < 0)
· (0; +∞)
· , "x > 0
· 
· TCN: trục Ox
 TCĐ: trục Oy
·
Chú ý: Khi khảo sát hàm số luỹ thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó.
VD1: Khảo sát sự biến thiên và vẽ đồ thị hàm số .
VD2: Khảo sát sự biến thiên và vẽ đồ thị hàm số 
Phương thức tổ chức: Cá nhân – tại lớp.
*Thực hiện theo các bước khảo sát và vẽ đồ thị hàm số
 (a > 0)
· (0; +∞)
· , "x > 0
· 
· Không có
·
KQ1
· D = (0; +∞)
· < 0, "x Î D
· TCĐ: x = 0; TCN: y = 0
· BBT:
· Đồ thị
KQ2
· D = R \ {0}
· < 0, "x Î D
· TCĐ: x = 0; TCN: y = 0
· BBT:
· Đồ thị
Hàm số là hàm số lẻ nên đồ thị nhận gốc toạ độ làm tâm đối xứng.
HOẠT ĐỘNG LUYỆN TẬP
C
HOẠT ĐỘNG VẬN DỤNG, TÌM TÒI MỞ RỘNG
D,E
BÀI TẬP TRẮC NGHIỆM:
Phần 1: Nhận biết – Thông hiểu 
Tập xác định của hàm số là:
A.	B. 	C. 	D. 
Tập xác định của hàm số là:
A.	B. 
C. 	D. 
Tập xác định của hàm số là:
A. 	B. 
C. 	D. 
Hàm số có đạo hàm là:
A.	B. 	C. 	D. 
Phần 2: Vận dụng thấp
Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A.	Hàm số có tập xác định là .
B.	Đồ thị hàm số với không có tiệm cận.
C.	Hàm số với nghịch biến trên khoảng .
D.	Đồ thị hàm số với có hai tiệm cận.
ĐÁP ÁN:
Chọn đáp án A
Vì nên hàm số xác định với mọi . 
Chọn đáp án A
Vì nên hàm số xác định khi . 
Chọn đáp án A
Vì nên hàm số xác định khi . 
 . 
Chọn đáp án A theo công thức tính đạo hàm.
 . 
Chọn đáp án A
Hàm số có tập xác định thay đổi tùy theo .